Embibe Experts Solutions for Chapter: Work, Energy and Power, Exercise 4: Exercise-4
Embibe Experts Physics Solutions for Exercise - Embibe Experts Solutions for Chapter: Work, Energy and Power, Exercise 4: Exercise-4
Attempt the practice questions on Chapter 8: Work, Energy and Power, Exercise 4: Exercise-4 with hints and solutions to strengthen your understanding. Beta Question Bank for Engineering: Physics solutions are prepared by Experienced Embibe Experts.
Questions from Embibe Experts Solutions for Chapter: Work, Energy and Power, Exercise 4: Exercise-4 with Hints & Solutions
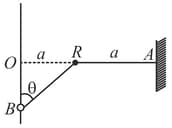
A small bead of mass is free to slide on a fixed smooth vertical wire, as indicated in the diagram. One end of a light elastic string, of unstretched length and force constant is attached to . The string passes through a smooth fixed ring and the other end of the string is attached to the fixed point , being horizontal. The point on the wire is at same horizontal level as , and .
(i) In the equilibrium position, find .
(ii) The bead is raised to a point of the wire above , where , and is released from rest. Find the speed of the bead as it passes , and find the greatest depth below of the bead in the subsequent motion.
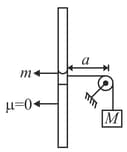
A ring of mass slides on a smooth vertical rod. A light string is attached to the ring and is passing over a smooth peg distant a from the rod, and at the other end of the string is a mass . The ring is held on a level with the peg and released. Show that it first comes to rest after falling a distance .
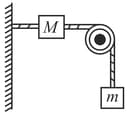
A string, with one end fixed on a rigid wall, passing over a fixed frictionless pulley at a distance of from the wall, has a point mass attached to it at a distance of from the wall. A mass attached at the free end is held at rest so that the string is horizontal between the wall and the pulley and vertical beyond the pulley. What will be the speed with which the mass will hit the wall when the mass is released?
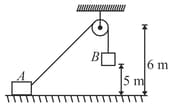
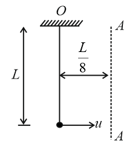
'' block of mass is held at rest on a smooth horizontal floor. A light frictionless, small pulley is fixed at a height of from the floor. A light inextensible string of length , connected with passes over the pulley and another identical block is hung from the string. Initial height of is from the floor as shown in figure. When the system is released from rest, starts to move vertically downwards and slides on the floor towards right. (i) If at an instant string makes an angle with horizontal, calculate relation between velocity of and of B (ii) Calculate when strikes the floor.
A particle is suspended vertically from a point by an inextensible massless string of length .A vertical line is at a distance from as shown in figure. The object is given a horizontal velocity . At some point, its motion ceases to be circular and eventually the object passes through the line . At the instant of crossing , its velocity is horizontal. Find .
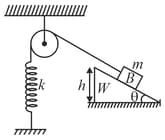
In the figure shown the pulley is smooth. The spring and the string are light. The block '' slides down from the along the fixed rough wedge of inclination . Assuming that the block reaches the end of the wedge. Find the speed of the block at the end. Take the coefficient of friction between the block and the wedge to be and the spring was relaxed when the block was released from the top of the wedge.
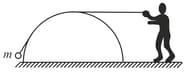
As shown in the figure a person is pulling a mass '' from ground on a fixed rough hemispherical surface upto the top of the hemisphere with the help of a light inextensible string. Find the work done by tension in the string if radius of hemisphere is and friction co-efficient is . Assume that the block is pulled with negligible velocity.
A small ring of mass is threaded on a horizontal smooth rod which is rotating about its end with constant angular velocity The ring is initially located at the axis of rotation. When the distance of the ring from the axis becomes , then find the power required to rotate the system with same angular velocity.
