Brijesh Dwevedi and Jitendra Gupta Solutions for Chapter: Surface Areas and Volumes, Exercise 3: Exam Practice

A hemispherical bowl is made of $0.50 \mathrm{cm}$ thick brass. The inner radius of the bowl is $6 \mathrm{cm}$. Find the inner and outer curved surface areas and volume of the bowl.

A spherical ball is divided into two equal halves. If the curved surface area of each half is $56.57 {\mathrm{cm}}^2$, then find the volume of the spherical ball.

To maintain beauty of a monument, the students of the school cleaned and painted the dome of the monument. The monument is in the form of a hemisphere. From inside, it was white washed by the students whose area is $249.48 {\mathrm{m}}^2$,  Find the volume of the air inside the dome.

To maintain beauty of a monument, the students of the school cleaned and painted the dome of the monument. The monument is in the form of a hemisphere. From inside, it was white washed by the students whose area is $249.48 {\mathrm{m}}^2$, find the volume of the air inside the dome, if white washing costs $₹2 \mathrm{per} {\mathrm{m}}^2$, how much does it costs?

A sector of a circle of radius $9 \mathrm{cm}$ and central angle of $120°$. It is rolled up so that the two bounding radii are joined together to form a cone.

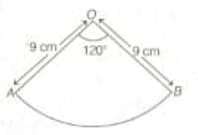
the slant height of the cone.

A sector of a circle of radius $9 \mathrm{cm}$ and central angle of $120°$. It is rolled up so that the two bounding radii are joined together to form a cone.

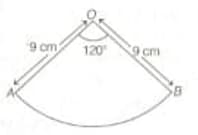
the radius of the base of the cone.

A sector of a circle of radius $9 \mathrm{cm}$ and central angle of $120°$. It is rolled up so that the two bounding radii are joined together to form a cone.

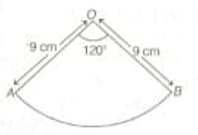
the volume of the cone.

A sector of a circle of radius $9 \mathrm{cm}$ and central angle of $120°$. It is rolled up so that the two bounding radii are joined together to form a cone.

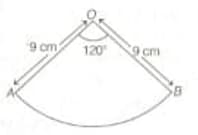
the total surface area of the cone.