M L Aggarwal Solutions for Chapter: Areas Related to Circles, Exercise 2: Exercise 13.2

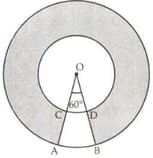
In the adjoining figure, two concentric circles with centre O have radii 21 cm and 42 cm. If ZAOB = 60°, find the area of the shaded region.

A calf is tied with a rope of length 6 m at the corner of a square grassy lawn of side 20 m. If the length of the rope is increased by 5.5 m, find the increase in area of the grassy lawn in which the calf can graze.

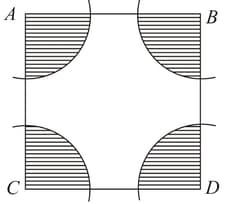
In figure, arcs have been down of radius $21 \mathrm{cm}$ each with vertices $A, B, C$ and $D$ of quadrilateral $ABCD$ as centres. Find the area of the shaded region. 

A chord of a circle of radius $14 \mathrm{cm}$ subtends an angle of $60$ at the centre. Find the area of the corresponding minor segment of the circle. $\left[\text{Use} \mathrm{\pi }=\frac{22}{7} \text{and} \sqrt{3}=1.73\right]$

In a circle of radius $21 \mathrm{cm}$, an arc subtends an angle of $60°$ at the centre. Find the length of the arc.

In a circle of radius $21 \mathrm{cm}$, an arc subtends an angle of $60°$ at the centre. Find the area of the sector formed by the arc.

In a circle of radius $21 \mathrm{cm}$, an arc subtends an angle of $60°$ at the centre. Find area of the segment formed by the corresponding chord.

A chord of a circle of radius $12 \mathrm{c}\mathrm{m}$ subtends an angle of ${120}^{\mathrm{o}}$ at the centre. Find the areas of the corresponding segment of the circle. ( Use $\pi =3.14$ and $\sqrt{3}=1.73$ )