Karen Morrison and Nick Hamshaw Solutions for Exercise 5: Examination practice

Dan either walks or cycles to school. The probability that he cycles to school is $\frac{1}{3}$. When Dan cycles to school the probability that he is late is $\frac{1}{8}$. Calculate the probability that Dan is not late.

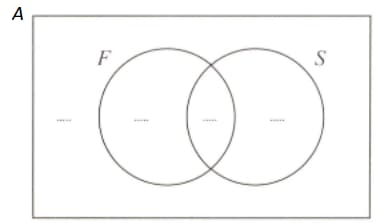
$A=${$25$ students in a class}

$F=${students who study French}

$S=${students who study Spanish}

$16$ students study French and $18$ students study Spanish. $2$ students study neither of these. Complete the Venn diagram to show this information.

$A=${$25$ students in a class}

$F=${students who study French}

$S=${students who study Spanish}

$16$ students study French and $18$ students study Spanish. $2$ students study neither of these. Find $n\left(F\text{'}\right)$.

$A=${$25$ students in a class}

$F=${students who study French}

$S=${students who study Spanish}

$16$ students study French and $18$ students study Spanish. $2$ students study neither of these. Find $n\left(F\cap S\right)\text{'}$.

$A=${$25$ students in a class}

$F=${students who study French}

$S=${students who study Spanish}

$16$ students study French and $18$ students study Spanish. $2$ students study neither of these. One student is chosen at random. Find the probability that this student studies both French and Spanish.

$A=${$25$ students in a class}

$F=${students who study French}

$S=${students who study Spanish}

$16$ students study French and $18$ students study Spanish. $2$ students study neither of these. Two students are chosen at random without replacement. Find the probability that they both study only Spanish

In a class the students all study at least one language from French, German and Spanish. No student studies all three languages. The set of student who study German is a proper subset of the set of students who study French. $4$ students study both French and German. $12$ students study Spanish but not French. $9$ students study French but not Spanish. A total of $16$ students study French. Draw a Venn Diagram to represent this information.

In a class the students all study at least one language from French, German and Spanish. No student studies all three languages. The set of student who study German is a proper subset of the set of students who study French. $4$ students study both French and German. $12$ students study Spanish but not French. $9$ students study French but not Spanish. A total of $16$ students study French. Find the total number of students in the class.