Jan Dangerfield, Stuart Haring and, Julian Gilbey Solutions for Exercise 7: END-OF-CHAPTER REVIEW EXERCISE 9

A light inextensible rope has a block $A$ of mass $5 \mathrm{kg}$ attached at one end, and a block $B$ of mass $16 \mathrm{kg}$ attached at the other end. The rope passes over a smooth pulley which is fixed at the top of a rough plane inclined at an angle of $30°$ to the horizontal. Block $A$ is held at rest at the bottom of the plane and block $B$ hangs below the pulley (see diagram). The coefficient of friction between $A$ and the plane is $\frac{1}{\sqrt{3}}$. Block $A$ is released from rest and the system starts to move. When each of the blocks has moved a distance of $x \mathrm{m}$ each has speed $v \mathrm{m}{ \mathrm{s}}^{-1}$.

Write down the gain in kinetic energy of the system in terms of $v$.

A light inextensible rope has a block $A$ of mass $5 \mathrm{kg}$ attached at one end, and a block $B$ of mass $16 \mathrm{kg}$ attached at the other end. The rope passes over a smooth pulley which is fixed at the top of a rough plane inclined at an angle of $30°$ to the horizontal. Block $A$ is held at rest at the bottom of the plane and block $B$ hangs below the pulley (see diagram). The coefficient of friction between $A$ and the plane is $\frac{1}{\sqrt{3}}$. Block $A$ is released from rest and the system starts to move. When each of the blocks has moved a distance of $x \mathrm{m}$ each has speed $v \mathrm{m}{ \mathrm{s}}^{-1}$.

Find, in terms of $x$,

the loss of gravitational potential energy of the system,

A light inextensible rope has a block $A$ of mass $5 \mathrm{kg}$ attached at one end, and a block $B$ of mass $16 \mathrm{kg}$ attached at the other end. The rope passes over a smooth pulley which is fixed at the top of a rough plane inclined at an angle of $30°$ to the horizontal. Block $A$ is held at rest at the bottom of the plane and block $B$ hangs below the pulley (see diagram). The coefficient of friction between $A$ and the plane is $\frac{1}{\sqrt{3}}$. Block $A$ is released from rest and the system starts to move. When each of the blocks has moved a distance of $x \mathrm{m}$ each has speed $v \mathrm{m}{ \mathrm{s}}^{-1}$.

Find, in terms of $x$,

the work done against the frictional force.

A light inextensible rope has a block $A$ of mass $5 \mathrm{kg}$ attached at one end, and a block $B$ of mass $16 \mathrm{kg}$ attached at the other end. The rope passes over a smooth pulley which is fixed at the top of a rough plane inclined at an angle of $30°$ to the horizontal. Block $A$ is held at rest at the bottom of the plane and block $B$ hangs below the pulley (see diagram). The coefficient of friction between $A$ and the plane is $\frac{1}{\sqrt{3}}$. Block $A$ is released from rest and the system starts to move. When each of the blocks has moved a distance of $x \mathrm{m}$ each has speed $v \mathrm{m}{ \mathrm{s}}^{-1}$.

Show that $21v^2=220x$.

Particle $W$, of mass $3 \mathrm{kg}$, and particle $X$, of mass $5 \mathrm{kg}$, are attached to the ends of a light, inextensible string of length $4 \mathrm{m}$. The string passes over a small smooth pulley fixed at the top of a fixed triangular wedge, $ABC$. The angles $BAC$ and $BCA$ are each $45°$ and the side $AC$ is fixed to horizontal ground. The distance from $A$ to $C$ is $3\sqrt{2} \mathrm{m}$. Surface $AB$ is smooth and surface $BC$ is rough, with coefficient of friction $\frac{1}{\sqrt{8}}$ Particle $W$ is held at the bottom of the slope $AB$ and is then gently released.

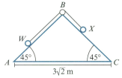
Find the work done against friction when particle $X$ moves a distance $x \mathrm{m}$.

Particle $W$, of mass $3 \mathrm{kg}$, and particle $X$, of mass $5 \mathrm{kg}$, are attached to the ends of a light, inextensible string of length $4 \mathrm{m}$. The string passes over a small smooth pulley fixed at the top of a fixed triangular wedge, $ABC$. The angles $BAC$ and $BCA$ are each $45°$ and the side $AC$ is fixed to horizontal ground. The distance from $A$ to $C$ is $3\sqrt{2} \mathrm{m}$. Surface $AB$ is smooth and surface $BC$ is rough, with coefficient of friction $\frac{1}{\sqrt{8}}$ Particle $W$ is held at the bottom of the slope $AB$ and is then gently released.

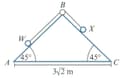
Find the change in the total potential energy when particle $X$ moves a distance $x \mathrm{m}$.

Particle $W$, of mass $3 \mathrm{kg}$, and particle $X$, of mass $5 \mathrm{kg}$, are attached to the ends of a light, inextensible string of length $4 \mathrm{m}$. The string passes over a small smooth pulley fixed at the top of a fixed triangular wedge, $ABC$. The angles $BAC$ and $BCA$ are each $45°$ and the side $AC$ is fixed to horizontal ground. The distance from $A$ to $C$ is $3\sqrt{2} \mathrm{m}$. Surface $AB$ is smooth and surface $BC$ is rough, with coefficient of friction $\frac{1}{\sqrt{8}}$ Particle $W$ is held at the bottom of the slope $AB$ and is then gently released.

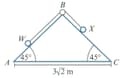
Use the work-energy principle to find the speed of the particles when particle $X$ reaches the ground at $C$.

Particle $W$, of mass $3 \mathrm{kg}$, and particle $X$, of mass $5 \mathrm{kg}$, are attached to the ends of a light, inextensible string of length $4 \mathrm{m}$. The string passes over a small smooth pulley fixed at the top of a fixed triangular wedge, $ABC$. The angles $BAC$ and $BCA$ are each $45°$ and the side $AC$ is fixed to horizontal ground. The distance from $A$ to $C$ is $3\sqrt{2} \mathrm{m}$. Surface $AB$ is smooth and surface $BC$ is rough, with coefficient of friction $\frac{1}{\sqrt{8}}$ Particle $W$ is held at the bottom of the slope $AB$ and is then gently released.

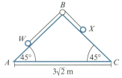
Explain why the work done by the tension does not need to be included in the work-energy calculation.