Dean Chalmers and Julian Gilbey Solutions for Chapter: Measures of Variation, Exercise 6: EXERCISE 3B
Dean Chalmers Mathematics Solutions for Exercise - Dean Chalmers and Julian Gilbey Solutions for Chapter: Measures of Variation, Exercise 6: EXERCISE 3B
Attempt the practice questions on Chapter 3: Measures of Variation, Exercise 6: EXERCISE 3B with hints and solutions to strengthen your understanding. Cambridge International AS & A Level Mathematics : Probability & Statistics 1 Course Book solutions are prepared by Experienced Embibe Experts.
Questions from Dean Chalmers and Julian Gilbey Solutions for Chapter: Measures of Variation, Exercise 6: EXERCISE 3B with Hints & Solutions
Kristina plans to raise money for charity. Her plan is to walk in days so that she walks on the th day. Find the standard deviation of the daily distances she plans to walk, and compare this with the interquartile range.
The mass of waste produced by a school during its three -week terms is given in tonnes, correct to decimal places, in the following table
| Mass of waste (tonnes) | ||||
| No. weeks |
Calculate estimates of the mean and standard deviation of the mass of waste produced per week, giving both answers correct to decimal places
The mass of waste produced by a school during its three -week terms is given in tonnes, correct to decimal places, in the following table
| Mass of waste (tonnes) | ||||
| No. of weeks |
Calculate estimates of the mean and standard deviation of the mass of waste produced per week, giving both answers correct to decimal places
No waste is produced in the weeks of the year that the school is closed. If this additional data is included in the calculations, what effect does it have on the mean and on the standard deviation?
The ages, in whole numbers of years, of a hotel's staff are given in the following table. Calculated estimates of the mean and variance are and respectively.
| Age (years) | ||||
| No. staff |
Exactly year after these calculations were made, Gudrun became the st staff member and the mean age became exactly years. Find Gudrun's age on the day of her recruitment, and determine what effect this had on the variance of the staff's ages. What assumptions must be made to justify your answers?
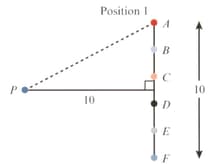
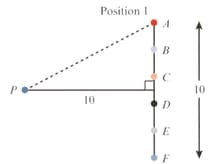
Refer to the following diagram. In position a -metre rod is placed metres from a fixed point, Six small discs, to are evenly spaced along the length of the rod. The rod is rotated anti-clockwise about its centre by to position The distances from to the discs are denoted by
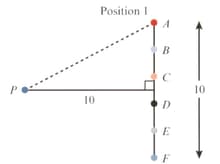
What effect does the rotation have on values of ? Investigate this by first considering the effect on the average distance from to the discs.
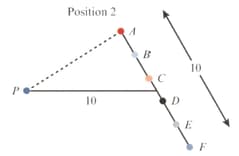
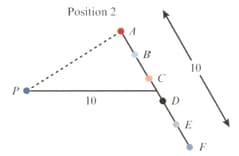
Refer to the following diagram. In position a -metre rod is placed metres from a fixed point, Six small discs, to are evenly spaced along the length of the rod. The rod is rotated anti-clockwise about its centre by to position The distances from to the discs are denoted by
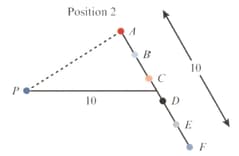
Find two values that can be used as measures of the change in the variation of caused by the rotation.
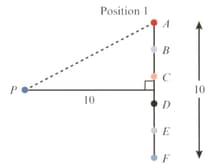
Refer to the following diagram. In position a -metre rod is placed metres from a fixed point, Six small discs, to are evenly spaced along the length of the rod. The rod is rotated anti-clockwise about its centre by to position The distances from to the discs are denoted by
Use the values obtained in parts and to summarise the changes in the distances from to the discs caused by the rotation.
Refer to the following diagram. In position a -metre rod is placed metres from a fixed point, Six small discs, to are evenly spaced along the length of the rod. The rod is rotated anti-clockwise about its centre by to position The distances from to the discs are denoted by
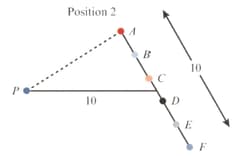
Can you prove that is constant for all values of
