Dean Chalmers and Julian Gilbey Solutions for Chapter: Representation of Data, Exercise 6: EXERCISE 1C

The diameters, $d \mathrm{cm}$, of $60$ cylindrical electronic components are represented in the following cumulative frequency graph.

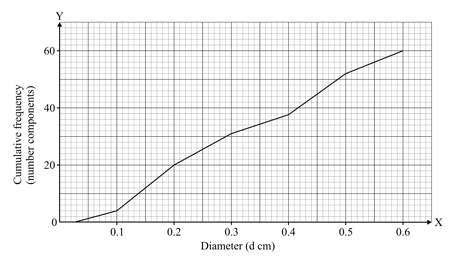
                                                                Diameter $(d \mathrm{cm})$

Estimate the number of components that have:
a diameter of less than $0.15 \mathrm{cm}$

The diameters, $d \mathrm{cm}$, of $60$ cylindrical electronic components are represented in the following cumulative frequency graph.

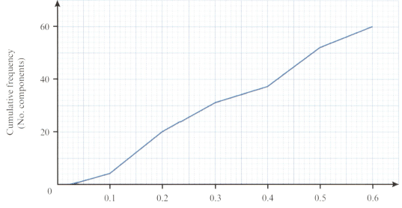
                                                                Diameter $(d \mathrm{cm})$

Estimate the number of components that have:
a radius of $0.16 \mathrm{cm}$ or more.

The daily journey times for $80$ bank staff to get to work are given in the following table.

How many staff take between $15$ and $45$ minutes to get to work?

The daily journey times for $80$ bank staff to get to work are given in the following table.

Find the exact number of staff who take$\frac{x+y}{2}$ minutes or more to get to work, given that $85\%$ of the staff take less than $x$ minutes and that $70\%$ of the staff take $y$ minutes or more.

The distances, in $\mathrm{km}$, that $80$ new cars can travel on $1$ litre of fuel are shown in the table.

These distances are $10\%$ greater than the distances the cars will be able to travel after they have covered more than $100000 \mathrm{km}$.

Estimate how many of the cars can travel $10.5 \mathrm{km}$ or more on $1$ litre of fuel when new, but not after they have covered more than $100000 \mathrm{km}$.

A small company produces cylindrical wooden pegs for making garden chairs. The lengths and diameters of the $242$ pegs produced yesterday have been measured independently by two employees, and their results are given in the following table.

On the same axes, draw two cumulative frequency graphs: one for lengths and one for diameters.

A small company produces cylindrical wooden pegs for making garden chairs. The lengths and diameters of the $242$ pegs produced yesterday have been measured independently by two employees, and their results are given in the following table.

On the same axes, draw two cumulative frequency graphs: one for lengths and one for diameters.

Correct to the nearest millimetre, the lengths and diameters of $n$ of these pegs are equal. Find the least and greatest possible value of $n$.

A small company produces cylindrical wooden pegs for making garden chairs. The lengths and diameters of the $242$ pegs produced yesterday have been measured independently by two employees, and their results are given in the following table.

On the same axes, draw two cumulative frequency graphs: one for lengths and one for diameters.

Correct to the nearest millimetre, the lengths and diameters of $n$ of these pegs are equal. Find the least and greatest possible value of $n$.

A peg is acceptable for use when it satisfies both $l⩾2.8$ and $d<2.2$. Explain why you cannot obtain from your graphs an accurate estimate of the number of these $242$ pegs that are acceptable. Suggest what the company could do differently so that an accurate estimate of the proportion of acceptable pegs could be obtained.