Sue Pemberton Solutions for Chapter: Further Differentiation, Exercise 8: EXERCISE 8E
Sue Pemberton Mathematics Solutions for Exercise - Sue Pemberton Solutions for Chapter: Further Differentiation, Exercise 8: EXERCISE 8E
Attempt the practice questions on Chapter 8: Further Differentiation, Exercise 8: EXERCISE 8E with hints and solutions to strengthen your understanding. Cambridge International AS & A Level Mathematics : Pure Mathematics 1 Course Book solutions are prepared by Experienced Embibe Experts.
Questions from Sue Pemberton Solutions for Chapter: Further Differentiation, Exercise 8: EXERCISE 8E with Hints & Solutions
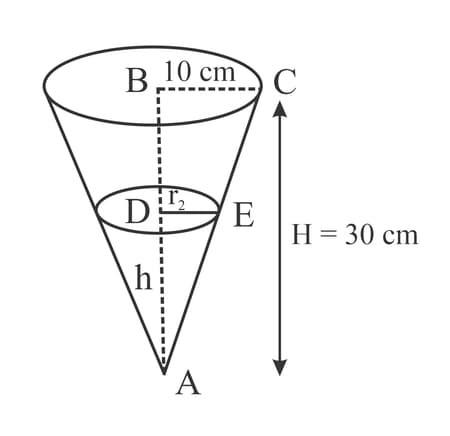
The diagram shows a right circular cone with radius cm and height cm. The cone is initially completely filled with water. Water leaks out of the cone through a small hole at the vertex at a rate of . Show that the volume of water in the cone, , when the height of the water is cm is given by the formula .
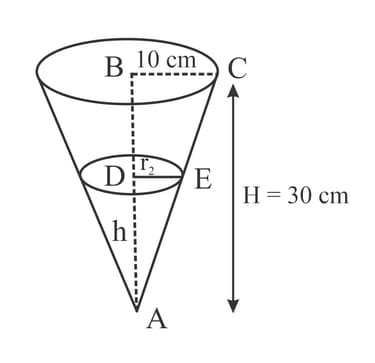
The diagram shows a right circular cone with radius cm and height cm. The cone is initially completely filled with water. Water leaks out of the cone through a small hole at the vertex at a rate of . Find the rate of change of , when cm.
Oil is poured onto a flat surface and a circular patch is formed. The radius of the patch increases at a rate of . Find the rate at which the area is increasing when the circumference is .
Paint is poured onto a flat surface and a circular patch is formed. The area of the patch increases at a rate of . Find, in terms of , the radius of the patch after seconds.
Paint is poured onto a flat surface and a circular patch is formed. The area of the patch increases at a rate of . Find, in terms of , the rate of increase of the radius of the patch after seconds.
A cylindrical container of radius cm and height cm is completely filled with water. The water is then poured at a constant rate from the cylinder into an empty inverted cone.The cone has radius cm and height cm and its axis is vertical. It takes seconds for all of the water to be transferred. If represents the volume of water, in , in the cone at time seconds, find in terms of .
A cylindrical container of radius cm and height cm is completely filled with water. The water is then poured at a constant rate from the cylinder into an empty inverted cone.The cone has radius cm and height cm and its axis is vertical. It takes seconds for all of the water to be transferred. When the depth of the water in the cone is cm, find the rate of change of the height of the water in the cone.
A cylindrical container of radius cm and height cm is completely filled with water. The water is then poured at a constant rate from the cylinder into an empty inverted cone.The cone has radius cm and height cm and its axis is vertical. It takes seconds for all of the water to be transferred. When the depth of the water in the cone is cm, Find the rate of change of the horizontal surface area of the water in the cone.
