Chittaranjan Dasgupta and Asok Kumar Das Solutions for Chapter: Fluid Dynamics, Exercise 1: EXERCISE

If a ball of steel (density $\rho =7.8 {\mathrm{gcm}}^{-3}$) attains a terminal velocity of $10 {\mathrm{cms}}^{-1}$ when falling in a tank of water (coefficient of viscosity $\eta =8.5\times {10}^{-4} P_a-s$) water then its terminal velocity in glycerine $\left(\rho =1.2 {\mathrm{gcm}}^{-3}, \eta =13.2 P_a-s\right)$ would be nearly?

A spherical solid ball of volume $V$ is made of a material of density ${\rho }_1$. It is falling through a liquid of density ${\rho }_2\left({\rho }_2<{\rho }_1\right)$. [Assume that the liquid applies a viscous force on the ball that is proportional to the square of its speed $v$, i.e. $F_{\mathrm{viscous}}=-\hat{k}{v}^2(k>0)$]. The terminal speed of the ball is

A cylindrical vessel of height $0.90 \mathrm{m}$ kept filled upto the brim. It has four holes $1, 2, 3, 4$ which are respectively at heights $0.20 \mathrm{m}, 0.30 \mathrm{m}, 0.40 \mathrm{m}$ and $0.50 \mathrm{m}$ from the horizontal floor. The tank is placed on that horizontal floor. The water falling at the maximum horizontal distance from the vessel comes from

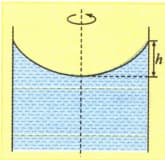
A liquid is kept in a cylindrical vessel which is rotated about its axis. The liquid rises at the sides, Fig. $15.37$. If the radius of the vessel is $0.05 \mathrm{m}$ and the speed of rotation is $2 \mathrm{rev}/\mathrm{s}$, the difference in the height of the liquid at the centre of the vessel and its side is

A metal plate of area $0.1{ \mathrm{m}}^2$ rests on a layer of oil $6\times {10}^{-3} \mathrm{m}$ thick. A tangential force of ${10}^{-2} \mathrm{N}$ is applied on it to move it with a constant velocity of $6\times {10}^{-2} \mathrm{m}/\mathrm{s}$. The coefficient of viscosity of the liquid is

A liquid flows through a pipe of non-uniform crosssection. If $A_1$ and $A_2$ are the cross-sectional areas of the pipe at two points, the ratio of velocities of the liquid at these points will be

Water is flowing through a very narrow tube. The velocity of water below which the flow remains a streamline flow is known as

Water is filled in a cylindrical container to a height of $3 \mathrm{m}$. There is an orifice on the side of the container at a height $x \mathrm{m}$ from the base of the container. The ratio of the cross-sectional area of the orifice and the beaker is $0.1$. The square of the speed of the liquid coming out from the orifice is $\left(g=10 \mathrm{m}/{\mathrm{s}}^2\right)$