D. C. Pandey Solutions for Chapter: Thermometry, Thermal Expansion and Kinetic Theory of Gases, Exercise 2: Excercise 2

A vertical closed cylinder is separated into two parts by a frictionless piston of mass $m$ and of negligible thickness. The piston is free to move along the length of the cylinder. The length of the cylinder above the piston is $l_1$ and that below the piston is $l_2,$ such that $l_1>l_2$ Each part of the cylinder contains $n$ moles of an ideal gas at equal temperature $T$. If the piston is stationary, its mass $m$, will be given by (where, $R$ is universal gas constant and $g$ is the acceleration due to gravity)

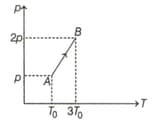
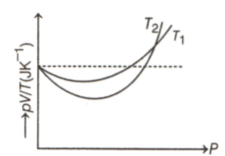
Pressure versus temperature graph of an ideal gas is shown in the given figure. Density of gas at point $A$ is ${\rho }_0$, then density of gas at point $B$ will be

The figure shows the graph of $\frac{pV}{T}$ versus $p$ for $2\times {10}^{-4} \mathrm{kg}$ of hydrogen gas at two different temperatures, where $p$, $V$ and $T$ represents pressure, volume and temperature respectively. Then, the value of $\frac{pV}{T},$ where the curve meet on the vertical axis, is

The wavelength of the radiation emitted by a black body is $1 \mathrm{mm}$ and Wien's constant is $3\times {10}^{-3} \mathrm{mK}$. Then the temperature of the black body will be,

An ideal gas in a closed container is heated so that the final $\mathrm{RMS}$ speed of the gas particles, increases by two times the initial speed. If the initial gas temperature is $27 °\mathrm{C},$ then What will be the final temperature of the ideal gas?

An ideal gas is taken through the cycle$A\to B\to C\to A$ as shown in the figure. If the net heat supplied to the gas in the cycle is $5 \mathrm{J}$. The magnitude of work done during the process $C\to A$ is

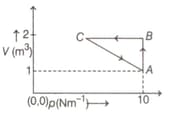
The maximum wavelength of radiation emitted by a star is $289.8 \mathrm{nm}$. Then intensity of radiation for the star is (Given : Stefan's constant is $5.67\times {10}^{-8}$ ${\mathrm{Wm}}^{-2} {\mathrm{K}}^{-4}$, Wien's constant, $b=2898 \mu \mathrm{mK}$)

Two black bodies $A$ and $B$ have equal surface areas and are maintained at temperatures $27 °\mathrm{C}$ and $177 °\mathrm{C}$, respectively. What will be the ratio of the thermal energy radiated per second by $A$ to that by $B$?