Motion in a Vertical Circle

A particle tied to a string describes a vertical circular motion of radius $r$ continually. If it has a velocity $\sqrt{3gr}$ at the highest point, then the ratio of the respective tensions in the string holding it at the highest and lowest points is

A bridge is in the form of a semi-circle of radius $40 \mathrm{m}$. The greatest speed with which a motorcycle can cross the bridge without leaving the ground at the highest point is $\left(g=10 \mathrm{m} {\mathrm{s}}^{-2}\right)$ (frictional force is negligibly small)

A small body of mass $m$ slides down from the top of a hemisphere of radius $r$. The surface of the block and hemisphere are frictionless.

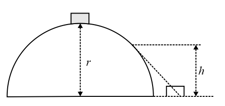
The height at which the body loses contact with the surface of the sphere is

A body of mass $m$ is rotated in a vertical circle of radius $r$. The minimum velocity of the body at the topmost position for the string to remain just stretched is

A particle rests on the top of a hemisphere of radius $R$. Find the smallest horizontal velocity that must be imparted to the particle if it is to leave the hemisphere without sliding down is

A sphere is suspended by a thread of length $l$. What minimum horizontal velocity has to be imparted to the sphere for it to reach the height of the suspension?

A block of mass $m$ at the end of a string is whirled round in a vertical circle of radius $r$. The critical speed of the block at the top of its swing below which the string would slacken before the block reaches the top is