D. C. Pandey Solutions for Chapter: Wave Motion, Exercise 7: Exercises

A long string, having a cross-sectional area $0.80 {\mathrm{mm}}^2$ and density $12.5 \mathrm{g} {\mathrm{cm}}^{-3}$, is subjected to a tension of $64 \mathrm{N}$ along the positive $x$-axis. One end of this string is attached to a vibrator at $x=0$, moving in the transverse direction at a frequency of $20 \mathrm{Hz}$. At $t=0$, the source is at maximum displacement, $y=1.0 \mathrm{cm}$.

(a) Find the speed of the wave traveling on the string.
(b) Write the equation for the wave.
(c) What is the displacement of the particle of the string at $x=50 \mathrm{cm}$ at time, $t=0.05 \mathrm{s}$?
(d) What is the velocity of this particle at this instant?

One end of each of two identical springs, each of force constant $0.5 \mathrm{N} {\mathrm{m}}^{-1}$, are attached on the opposite sides of a wooden block of mass $0.01 \mathrm{kg}$. The other ends of the springs are connected to separate rigid supports such that the springs are unstretched and are collinear in a horizontal plane. To the wooden piece is fixed a pointer which touches a vertically moving plane paper. The wooden piece kept on a smooth horizontal table is now displaced by $0.02 \mathrm{m}$ along the line of springs and released. If the speed of paper is $0.1 \mathrm{m} {\mathrm{s}}^{-1}$, find the equation of the path traced by the pointer on the paper and the distance between two consecutive maxima on this path.

A wave pulse is traveling on a string with a speed $v$ towards the positive $x$-axis. The shape of the string at $t=0$ is given by $y\left(x\right)=A\sin \left(\frac{x}{a}\right)$ where, $A$ and $a$ are constants.
(a) What are the dimensions of $A$ and $a$?
(b) Write the equation of the wave for a general time $t$ if the wave speed is $v$.

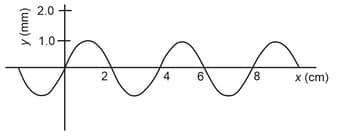
Figure shows a plot of the transverse displacement of the particle of a string at $t=0$ through which a traveling wave is passing in the positive $x$-direction. The wave speed is $20 \mathrm{cm} {\mathrm{s}}^{-1}$. Find (a) the amplitude (b) the wavelength (c) the wave number and (d) the frequency of the wave.

Two wires of different densities but same area of cross-section are soldered together at one end and are stretched to tension $T$. The velocity of a transverse wave in the first wire is double of that in the second wire. Find the ratio of the density of the first wire to that of the second wire.

Two long strings $A$ and $B$, each having linear mass density $1.2 \times {10}^{-2} \mathrm{kg} {\mathrm{m}}^{-1}$, are stretched by different tensions $4.8 \mathrm{N}$ and $7.5 \mathrm{N}$, respectively, and are kept parallel to each other with their left ends at $x=0$. Wave pulses are produced on the strings at the left ends at $t=0$ on string $A$ and at $\mathrm{t}=20 \mathrm{ms}$ on string $B$. When and where will the pulse on $B$ overtake that on $A$.

A sinusoidal transverse wave travels on a string. The string has length $8.00 \mathrm{m}$ and mass $6.00 \mathrm{g}$. The wave speed is $30.0 \mathrm{m} {\mathrm{s}}^{-1}$ and the wavelength is $0.200 \mathrm{m}$.

(a) If the wave is to have an average power of $50.0 \mathrm{W}$, what must be the amplitude of the wave?

(b) For this same string, if the amplitude and wavelength are the same as in part (a) what is the average power for the wave if the tension is increased such that the wave speed is doubled?

A uniform rope, with length $L$ and mass $m$, is held at one end and whirled in a horizontal circle with angular velocity $\mathrm{\omega }$. You can ignore the force of gravity on the rope. Find the time required for a transverse wave to travel from one end of the rope to the other.