Dean Chalmers and Julian Gilbey Solutions for Chapter: Probability, Exercise 10: END-OF-CHAPTER REVIEW EXERCISE 4

Bookings made at a hotel include a room plus any meal combination of breakfast $\left(B\right)$, lunch $\left(L\right)$ and supper $\left(S\right)$. The Venn diagram opposite shows the number of each type of booking made by $71$ guests on Friday.

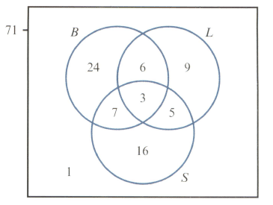
A guest who has not booked all three meals is selected at random. Find the probability that this guest:

has booked breakfast or supper

Bookings made at a hotel include a room plus any meal combination of breakfast $\left(B\right)$, lunch $\left(L\right)$ and supper $\left(S\right)$. The Venn diagram opposite shows the number of each type of booking made by $71$ guests on Friday.

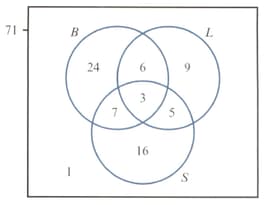
A guest who has not booked all three meals is selected at random. Find the probability that this guest:

has not booked supper, given that they have booked lunch.

Bookings made at a hotel include a room plus any meal combination of breakfast $\left(B\right)$, lunch $\left(L\right)$ and supper $\left(S\right)$. The Venn diagram opposite shows the number of each type of booking made by $71$ guests on Friday.

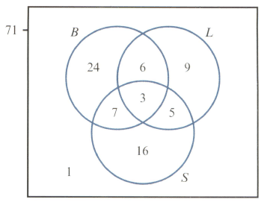
Find the probability that two randomly selected guests have both booked lunch, given that they have both booked at least two meals.

Three strangers meet on a train. Assuming that a person is equally likely to be born in any of the $12$ months of the year, find the probability that at least two of these three people were born in the same month of the year.

A box contains three black and four white chess pieces. Find the probability that a random selection of five chess pieces, taken one at a time without replacement, contains exactly two black pieces which are selected one immediately after the other.

The following table shows the numbers of IGCSE$\left(I\right)$ and $A$ Level $\left(A\right)$ examinations passed by a group of university students.

For a student selected at random, find:

$\mathrm{P}(\mathrm{I}+\mathrm{A}=11\mid \mathrm{A}<4)$

The following table shows the numbers of IGCSE$\left(I\right)$ and $A$ Level $\left(A\right)$ examinations passed by a group of university students.

For a student selected at random, find:

$\mathrm{P}(\mathrm{I}-\mathrm{A}>5\mid \mathrm{I}+\mathrm{A}>10)$

The following table shows the numbers of IGCSE$\left(I\right)$ and $A$ Level $\left(A\right)$ examinations passed by a group of university students.

Six students who all have at least three A Level passes are selected at random. Find the greatest possible range of the total number of IGCSE passes that they could have.