Dean Chalmers and Julian Gilbey Solutions for Chapter: Probability, Exercise 3: EXERCISE 4B

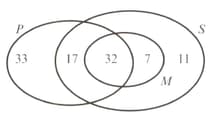
The $100$ students at a technical college must study at least one subject from Pure Mathematics $\left(P\right)$, Statistics $\left(S\right)$ and Mechanics $\left(M\right)$. The numbers studying these subjects are given in the diagram opposite.

Find the probability that a randomly selected student studies: Pure Mathematics or Mechanics.

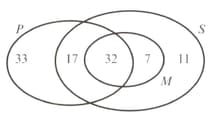
The $100$ students at a technical college must study at least one subject from Pure Mathematics $\left(P\right)$, Statistics $\left(S\right)$ and Mechanics $\left(M\right)$. The numbers studying these subjects are given in the diagram opposite.

Find the probability that a randomly selected student studies exactly two of these subjects.

Events $X$ and $Y$ are such that $\mathrm{P}\left(X\right)=0.5, \mathrm{P}\left(Y\right)=0.6$ and $\mathrm{P}(X\cap Y)=0.2$.

Find $\mathrm{P}(X\cup Y)$.

Events $X$ and $Y$ are such that $\mathrm{P}\left(X\right)=0.5, \mathrm{P}\left(Y\right)=0.6$ and $\mathrm{P}(X\cap Y)=0.2$.

Find the probability that $X$ or $Y$, but not both, occurs.

$A, B$ and $C$ are events where $\mathrm{P}\left(A\right)=0.3, \mathrm{P}\left(B\right)=0.4, \mathrm{P}\left(C\right)=0.3, \mathrm{P}(A\cap B)=0.12, \mathrm{P}(A\cap C)=0$ and $\mathrm{P}(B\cap C)=0.1$

Find $\mathrm{P}\left[(A\cup B\cup C{)}^{\text{'}}\right]$, which is the probability that neither $A$ nor $B$ nor $C$ occurs.

Given that $\mathrm{P}\left(A\right)=0.4, \mathrm{P}\left(B\right)=0.7$ and that $\mathrm{P}(A\cup B)=0.8$, find:

$\mathrm{P}\left(A\cup B^{\text{'}}\right)$

Given that $\mathrm{P}\left(A\right)=0.4, \mathrm{P}\left(B\right)=0.7$ and that $\mathrm{P}(A\cup B)=0.8$, find:

$\mathrm{P}\left({\mathrm{A}}^{\text{'}}\cap \mathrm{B}\right)$

Each of $27$ tourists was asked which of the countries Angola $\left(A\right)$, Burundi $\left(B\right)$ and Cameroon $\left(C\right)$ they had visited. Of the group, $15$ had visited Angola; $8$ had visited Burundi; $12$ had visited Cameroon; $12$ had visited all three countries; and $21$ had visited only one. Of those who had visited Angola, $4$ had visited only one other country. Of those who had not visited Angola, $5$ had visited Burundi only. All of the tourists had visited at least one of these countries.

Find the probability that a randomly selected tourist from this group had visited at least two of these three countries.