Embibe Experts Solutions for Chapter: Rotational Motion, Exercise 1: JEE Advanced Paper 2 - 2016
Embibe Experts Physics Solutions for Exercise - Embibe Experts Solutions for Chapter: Rotational Motion, Exercise 1: JEE Advanced Paper 2 - 2016
Attempt the free practice questions on Chapter 6: Rotational Motion, Exercise 1: JEE Advanced Paper 2 - 2016 with hints and solutions to strengthen your understanding. EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR PHYSICS solutions are prepared by Experienced Embibe Experts.
Questions from Embibe Experts Solutions for Chapter: Rotational Motion, Exercise 1: JEE Advanced Paper 2 - 2016 with Hints & Solutions
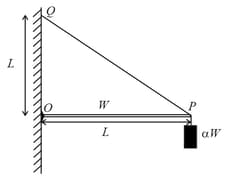
One end of a horizontal uniform beam of weight and length is hinged on a vertical wall at point and its other end is supported by a light inextensible rope. The other end of the rope is fixed at point , at a height above the hinge at point . A block of weight is attached at the point of the beam, as shown in the figure (not to scale). The rope can sustain a maximum tension of . Which of the following statement(s) is(are) correct?
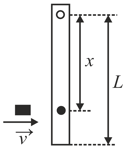
A rod of mass and length pivoted at one of its ends, is hanging vertically. A bullet of the same mass moving at speed strikes the rod horizontally at a distance from its pivoted end and gets embedded in it. The combined system now rotates with an angular speed about the pivot. The maximum angular speed is achieved for . Then
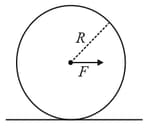
A horizontal force is applied at the centre of mass of a cylindrical object of mass and radius , perpendicular to its axis as shown in the figure. The coefficient of friction between the object and the ground is . The centre of mass of the object has an acceleration . The acceleration due to gravity is . Given that the object rolls without slipping, which of the following statement(s) is (are) correct?
A particle of mass is initially at rest in the -plane at a point , where and . The particle is accelerated at time with a constant acceleration along the positive -direction. Its angular momentum and torque with respect to the origin, in SI units, are represented by and , respectively. and are unit vectors along the positive and -directions, respectively. If then which of the following statement(s) is (are) correct?
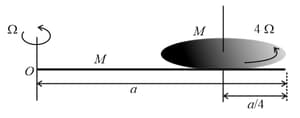
A thin rod of mass and length is free to rotate in horizontal plane about a fixed vertical axis passing through point . A thin circular disc of mass and of radius is pivoted on this rod with its centre at a distance from the free end so that it can rotate freely about its vertical axis, as shown in the figure. Assume that both the rod and the disc have uniform density and they remain horizontal during the motion. An outside stationary observer finds the rod rotating with an angular velocity and the disc rotating about its vertical axis with angular velocity . The total angular momentum of the system about the point is .
The value of is _________ .
A football of radius is kept on a hole of radius made on a plank kept horizontally. One end of the plank is now lifted so that it gets tilted making an angle from the horizontal as shown in the figure below. The maximum value of so that the football does not start rolling down the plank satisfies (figure is schematic and not drawn to scale)
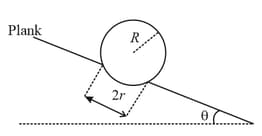
A small roller of diameter has an axle of diameter (see figure below on the left). It is on a horizontal floor and a meter scale is positioned horizontally on its axle with one edge of the scale on top of the axle (see figure on the right). The scale is now pushed slowly on the axle so that it moves without slipping on the axle, and the roller starts rolling without slipping. After the roller has moved the position of the scale will look like (figures are schematic and not drawn to scale)
A ring and a disc are initially at rest, side by side, at the top of an inclined plane which makes an angle with the horizontal. They start to roll without slipping at the same instant of time along the shortest path. If the time difference between their reaching the ground is , then the height of the top of the inclined plane (in meters) is __________. Take .
