Embibe Experts Solutions for Chapter: Gravitation, Exercise 3: Exercise - 3

Two particles of equal mass $m$go around a circle of radius $R$ under the action of their mutual gravitational attraction. The speed of each particle with respect to their centre of mass is: 

The mass of a spaceship is $1000 \mathrm{kg}.$ It is to be launched from the earth's surface out into free space. The value of$g$ and $R$ (radius of earth) are $10 \mathrm{m} {\mathrm{s}}^{-2}$ and $6400 \mathrm{km}$, respectively. The required energy for this work will be:

What is the minimum energy required to launch a satellite of mass $m$ from the surface of a planet of mass $M$ and radius $R$ in a circular orbit at an altitude of $2R$?

Four particles, each of mass $M$ on vertices of a square move along a circle of radius $R$ under the action of their mutual gravitational attraction. The speed of each particle is:

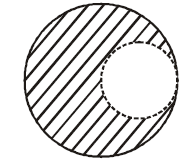
From a solid sphere of mass $M$ and radius $R$, a spherical portion of radius $R/2$ is removed as shown in the figure. Taking gravitational potential $V = 0 \mathrm{at} r = \infty ,$ the potential at the centre of the cavity thus formed is: ($G =$ gravitational constant)

A satellite is revolving in a circular orbit at a height$h$ from the earth’s surface (radius or earth $R$; $h<<R$). The minimum increase in its orbital velocity required, so that the satellite could escape from the earth’s gravitational field is close to: (Neglect the effect of atmosphere) 

The variation of acceleration due to gravity $g$ with distance d from centre of the earth is best represented by ($R=$ Earth's radius)

A particle is moving in a circular path of radius $a$, under the action of an attractive potential, $U=-\frac{K}{2r^2}$. Its total energy is