Embibe Experts Solutions for Chapter: Kinematics, Exercise 4: Exercise - 4

A small ball is thrown from the edge of one bank of a river of width $100 \mathrm{m}$ to just reach the other bank. The ball was thrown in the vertical plane (which is also perpendicular to the banks) at an angle $37º$ to the horizontal. Taking the starting point as the origin $O$, vertically upward direction as positive $y$-axis and the horizontal line passing through the point $O$ and perpendicular to the bank as $x$-axis find

 (a) equation of trajectory of the image formed by refraction by the water surface (water surface is at the level $y=0$)

(b) The instantaneous velocity of the image formed due to refraction. $\left(g=10 \mathrm{m} {\mathrm{s}}^{-2} , n_{\mathrm{water}}=\frac{4}{3}\right)$.

A particle is projected from point $O$ on the ground with velocity $\mathrm{u}=5\sqrt{5} \mathrm{m} {\mathrm{s}}^{-1}$ at angle $\mathrm{\alpha }={\tan }^{–1}\left(0.5\right)$. It strikes at a point $\mathrm{C}$ on a fixed smooth plane $\mathrm{AB}$ having inclination of$37º$ with horizontal as shown in figure. If the particle does not rebound, calculate:

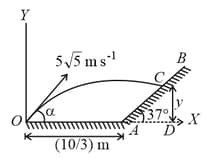
$\left(\mathrm{a}\right)$ coordinates of point C in reference to coordinate system as shown in the figure.

$\left(\mathrm{b}\right)$ maximum height from the ground to which the particle rises. $\left(\mathrm{g}=10 \mathrm{m} {\mathrm{s}}^{-2}\right)$

A monkey of mass $15 \mathrm{kg}$ is climbing on a rope with one end fixed to the ceiling . If it wishes to go up with an acceleration$1 \mathrm{m} {\mathrm{s}}^{-2}$, how much force should it apply to the rope? If the rope is $5 \mathrm{m}$ long and the monkey starts to rest, how much time will it take to reach the ceiling?

When a model rocket is launched, the propellant burns for a few seconds, accelerating the rocket upward. After burnout, the rocket moves upward for a while and then begins to fall. A parachute opens shortly after the rocket starts down. The parachute slows the rocket to keep it from breaking when it lands. The figure here shows velocity data from the flight of the model rocket. Use the data to answer the following.

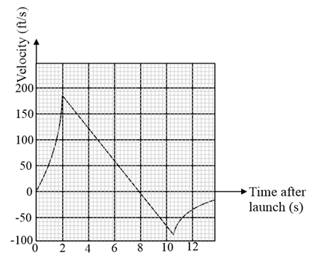
$\left(\mathrm{a}\right)$ How fast was the rocket climbing when the engine stopped? 

$\left(\mathrm{b}\right)$ For how many seconds did the engine burn?

$\left(\mathrm{c}\right)$ When did the rocket reach its highest point? What was its velocity then?

$\left(\mathrm{d}\right)$ When did the parachute open up? How fast was the rocket falling then?

$\left(\mathrm{e}\right)$ How long did the rocket fall before the parachute opened?

$\left(\mathrm{f}\right)$ When was the rocket's acceleration greatest?

$\left(\mathrm{g}\right)$ When was the acceleration constant? What was its value then (to the nearest integer)?

Two cars $A$ and $B$ are racing along straight line. Car $A$ is leading such that their relative velocity is directly proportional to the distance between the two cars. When the lead of car $A$ is $l_1=10 \mathrm{m}$, its running $10 \mathrm{m} {\mathrm{s}}^{-1}$ faster than car $B$. If the time car $A$ will take to increase its lead to $l_2=20 \mathrm{m}$ from car $B$ is $t=\left({\log }_{e}n\right) \sec$, then find $n$.

A large heavy box is sliding without friction down a smooth plane of inclination $\theta$. From a point $P$ on the bottom of the box, a particle is thrown inside the box. The initial speed of the particle with respect to the box is $u$ and the direction of projection makes an angle $\mathrm{\alpha }$ with the bottom as shown in the figure. 

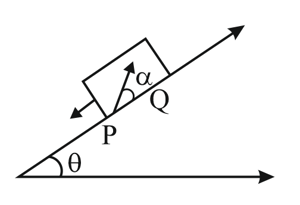
(a) Find the distance along the bottom of the box between the point of projection $P$ and the point $Q$ where the particle lands (assume that the particle does not hit any other surface of the box. Neglect air resistance).

(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero. Find the speed of the box with respect to the ground at the instant when the particle was projected.

A motorboat going downstream overcomes a raft (a wooden block) at a point $A\text{;} \tau =60 \min$. Later it turns back and after some time passes the boat and meets the raft at a distance $6.0 \mathrm{km}$ from the point $A$. Find the flow velocity assuming the duty of the engine to be constant.

An insect moves in a circular path of radius $R$. If it rotates through an angle $\theta$, find its displacement, $\overrightarrow{s}=\mathrm{\Delta }\overrightarrow{r}$, where, $\mathrm{\Delta }\overrightarrow{r}$ is the change in position vector.