Embibe Experts Solutions for Chapter: Laws of Motion, Exercise 4: Exercise - 4

In the arrangement shown in figure the masses of the wedge $M$ and the body $m$ are known. The appreciable friction exists only between the wedge and the body $m$, the friction coefficient being equal to $k$. The masses of the pulley and the thread are negligible. Find the acceleration of the body $m$ relative to the horizontal surface on which the wedge slides.

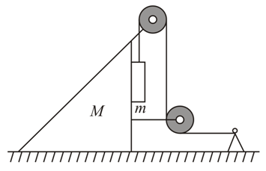
What is the minimum acceleration with which bar $A$ (figure) should be shifted horizontally to keep bodies $1$ and $2$ stationary relative to the bar? The masses of the bodies are equal and the coefficient of friction between the bar and the bodies is equal to $k$. The masses of the pulley and the threads are negligible, the friction in the pulley is absent.

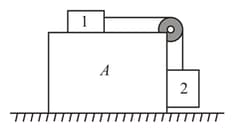
Prism $1$ with bar $2$ of mass $m$ placed on it gets a horizontal acceleration $a_0$ directed to the left (figure). At what maximum value of this acceleration will the bar be still stationary relative to the prism, if the coefficient of friction between them $k<\cot \alpha$?

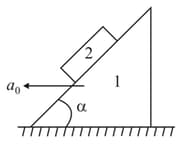
A small spherical ball undergoes an elastic collision with a rough horizontal surface. Before the collision, it is moving at an angle $\mathrm{\theta }$ to the horizontal (see figure). You may assume that the frictional force obeys the law $f=\mu N$during the contact period, where $N$ is the normal reaction on the ball and $\mu$ is the coefficient of friction.

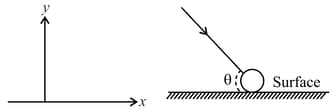
$\left(\mathrm{a}\right)$ Obtain ${\mathrm{\theta }}_{\mathrm{m}} \left(\mu \right)$, so that the subsequent horizontal range of the ball after leaving the horizontal surface is maximised.

$\left(\mathrm{b}\right)$ Find the allowed range for ${\mathrm{\theta }}_{\mathrm{m}}.$

The pulley (uniform disc) shown in figure has, radius $10 \mathrm{cm}$ and moment of inertia about its axis $I=0.5 \mathrm{kg} {\mathrm{m}}^2$ ($B$ and $A$ both move)

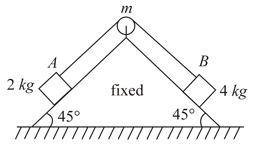
(a) Assuming all the plane surfaces are smooth and there is no slipping between pulley and string, calculate the acceleration of the mass $4 \mathrm{kg}$.

(b) The friction coefficient between the block $A$ and the plane below is $\mu =0.5$ and the plane below the $B$ block is frictionless. Assuming no slipping between pulley and string find acceleration of $4 \mathrm{kg}$ block. Take $g=10 \mathrm{m} {\mathrm{s}}^{-2}$.

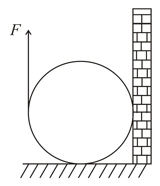
Figure shows a vertical force $F$ that is applied tangentially to a uniform cylinder of weight $W$. The coefficient of static friction between the cylinder and all surfaces is $0.5$. Find in terms of $W$, the maximum force that can be applied without causing the cylinder to rotate.

A wedge of mass $m$and triangular cross section $(AB=BC=CA=2R)$ is moving with a constant velocity-$v\hat{\mathrm{i}}$ towards a sphere of radius $R$ fixed on a smooth horizontal table as shown in the figure. The wedge makes an elastic collision with the fixed sphere and returns along the same path without any rotation. Neglect all friction and suppose that the wedge remains in contact with the sphere for a very short time $∆t$, during which the sphere exerts a constant force $\overrightarrow{F}$ on the wedge. The sphere is always fixed.

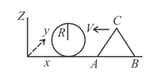
(a) Find the force $\overrightarrow{F}$ and also the normal force $\overrightarrow{N}$ exerted by the table on the wedge during the time $∆t$.

(b) Let $h$denote the perpendicular distance between the centre of mass of the wedge and the line of action of force $\overrightarrow{F}$. Find the magnitude of the torque due to the normal force $\overrightarrow{N}$ about the centre of the wedge, during the time $∆t$.

A particle of mass $m$ is moving in the $x-y$ plane such that its $x$ and $y$ coordinates vary according to the law, $x=a\mathrm{sin\omega }t \text{and} y=a\cos \omega t$ where $a$ and $\mathrm{\omega }$ are positive constants and $t$ is time. Find,

(a) equation of the path. Name the trajectory (path),

(b) whether the particle moves in clockwise or anticlockwise direction,

(c) magnitude of the force on the particle at any time $t$.