Embibe Experts Solutions for Chapter: Mathematical Tools in Physics, Exercise 1: Exercise - 1

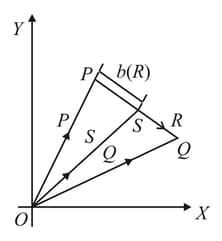
Three vectors $P, Q$ and $R$ are shown in the figure. Let $S$ be any point on the vector $R.$ The distance between the points $P$ and $S$ is $b\left[R\right].$ The general relation among vectors $P, Q$ and $S$ is,

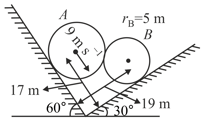
System is shown in the figure. Velocity of sphere $A$ is $9 \mathrm{m} {\mathrm{s}}^{-1}$. Then speed of sphere $B$ will be:

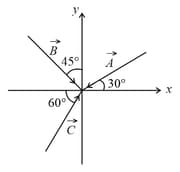
Vectors $\overrightarrow{A},\overrightarrow{ B}$ and $\overrightarrow{C}$ are shown in the figure. Find the angle between (i) $\overrightarrow{A}$ and $\overrightarrow{B}$, (ii) $\overrightarrow{A}$ and $\overrightarrow{C}$, and (iii) $\overrightarrow{B}$ and $\overrightarrow{C}$.

What are the $x$ and $y$ components of a $25 \mathrm{m}$ displacement which is at an angle of $210°$ with the $x$-axis (anti-clockwise)?

The vector $\overrightarrow{A}$ is of length $2\mathrm{cm}$ and is $60°$ above the $x‐$axis in the first quadrant. The vector $\overrightarrow{B}$ is of length $2\mathrm{cm}$ and $60°$ below the $x‐$axis in the fourth quadrant. The sum $\overrightarrow{A}+\overrightarrow{B}$ is a vector of magnitude

A vector $\overrightarrow{\mathit{A}}$ points vertically downward and $\overrightarrow{\mathit{B}}$ points towards the east, then the vector product $\overrightarrow{A}\times \overrightarrow{B}$ is

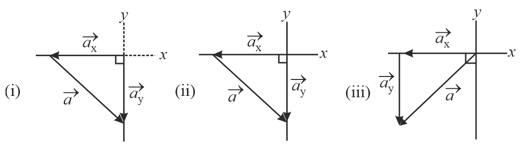
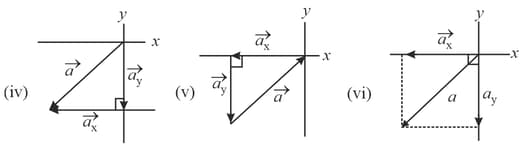
In the figure which of the ways indicated for combining the $x$ and $y$ components of the vector $\overrightarrow{a}$ are proper to determine that vector?

Let $\overrightarrow{\mathrm{a}}$ and $\overrightarrow{\mathrm{b}}$ be two non-null vectors such that $|\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}|=|\overrightarrow{\mathrm{a}}-2\overrightarrow{\mathrm{b}}|$. Then the value of $\frac{\left|\overrightarrow{\mathrm{a}}\right|}{\left|\overrightarrow{\mathrm{b}}\right|}$ maybe,