Embibe Experts Solutions for Chapter: Simple Harmonic Motion, Exercise 4: Exercise - 4

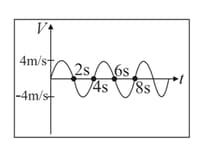
If velocity of a particle moving along a straight line changes sinusoidally with time as shown in the given graph, find the average speed over time interval, $t=0 \text{to} t=2(2n–1) \mathrm{s}$, $n$ being any positive integer.

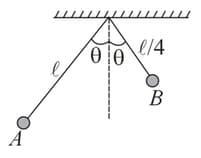
Two simple pendulums $A$ and $B$ having lengths $l$ and $\frac{l}{4}$, respectively, are released from the position as shown in figure. Calculate the time after which the release of the two strings become parallel for the first time. The angle $\mathrm{\theta }$is very small.

Two non–viscous, incompressible and immiscible liquids of densities $\mathrm{\rho }$ and $1.5 \mathrm{\rho }$ are poured into the two limbs of a circular tube of radius $\mathrm{R}$ and small cross–section kept fixed in a vertical plane as shown in fig. Each liquid occupies one–fourth the circumference of the tube.

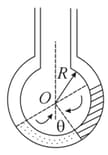
(a) Find the angle $\mathrm{\theta }$that the radius to the interface makes with the vertical in equilibrium position.

(b) If the whole liquid column is given a small displacement from its equilibrium position, show that the resulting oscillations are simple  harmonic. Find the time period of these oscillations.

Two identical balls $A$ and $B$, each of mass $0.1 \mathrm{kg}$, are attached to two identical massless springs. The spring–mass system is constrained to move inside a rigid smooth pipe bent in the form of a circle as shown in the figure. The pipe is fixed in a horizontal plane. The centres of the balls can move in a circle of radius $0.06 \mathrm{m}$. Each spring has a natural length of $0.06\mathrm{\pi } \mathrm{metre}$ and spring constant $0.1 \mathrm{N} {\mathrm{m}}^{-1}$. Initially, both the balls are displaced by an angle $\mathrm{\theta }=\frac{\mathrm{\pi }}{6}$ radian with respect to the diameter $PQ$ of the circle (as shown in fig.) and released from rest.

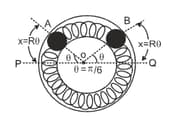
(i) Calculate the frequency of oscillation of ball $B$.

(ii) Find the speed of ball $A$ when $A$ and $B$ are at the two ends of the diameter $PQ$.

(iii) What is the total energy of the system?

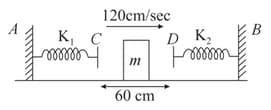
Two light springs of force constants $k_1$ and $k_2$ and a block of mass $m$ are in one line $AB$ on a smooth horizontal table such that one end of each spring is fixed to rigid supports and the other end is free as shown in the figure. The distance $CD$ between the free ends of the spring is $60 \mathrm{cm}$. If the block moves along $AB$ with a velocity $120 \mathrm{cm} {\mathrm{s}}^{-1}$ in between the springs, calculate the period of oscillation of the block $(k_1=1.8 \mathrm{N} {\mathrm{m}}^{-1}\text{,} k_2=3.2 \mathrm{N} {\mathrm{m}}^{-1}\text{,} m=200 \mathrm{g})$.

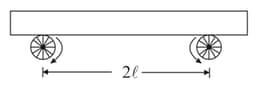
Two wheels which are rotated by some external source with constant angular velocity in opposite directions as shown in figure. A uniform plank of mass $\mathrm{M}$ is placed on it symmetrically. The friction coefficient between each wheel and the plank is $\mathrm{\mu }$. Find the frequency of oscillations, when plank is slightly displaced along its length and released.

The Cubic Potential: Consider a particle of mass $m$ moving in one dimension under the influence of potential energy $u\left(x\right)=\frac{m{\omega }^2{x}^2}{2}-\delta x-\frac{\alpha x^3}{3}$ Here $\mathrm{\omega }, \mathrm{\delta }$ and $\alpha$a are real and positive. 

(a) Sketch typical plots of $u\left(x\right)$ and identify extrema if any.

(b) Consider the case where (in appropriate units) we have $m= 1, \mathrm{\omega } = \sqrt{2} , \mathrm{\alpha } = 1$ and $\mathrm{\delta } = \frac{1}{2}.$ Sketch the potential energy $u\left(x\right)$. If the total energy of the particle moving in this one-dimensional potential is $E=0$ (in same units), discuss the motion of the particle in terms of allowed regions, boundedness and periodicity.

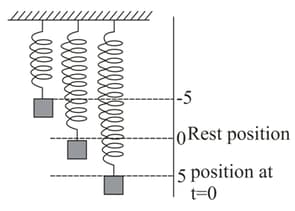
A body hanging from a spring (figure) is stretched $5 \mathrm{units}$ beyond its rest position and released at time $t=0$ to oscillate up and down. Its position at any later time $t$ is $s=5\cos t$. What are its velocity and acceleration at time $t$?