Exercise - 1

A capillary tube of the radius, $R$ is immersed in water, and water rises in it to a height, $H$. Mass of water in the capillary tube is $M$. If the radius of the tube is doubled, the mass of water that will rise in the capillary tube will now be

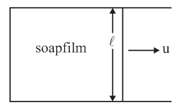
A soap film is created in a small wire frame as shown in the figure. The sliding wire of mass $m$ is given a velocity $u$ to the right and assume that $u$ is small enough so that film does not break. Plane of the film is horizontal and surface tension is $T$. Then time to regain the original position of wire is equal to :

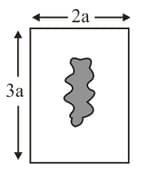
A rectangular massless blade (as shown in figure) is placed on a water surface (surface tension $T=\frac{1}{7}\times {10}^{-1} \mathrm{N} {\mathrm{m}}^{-1}$. Perimeter of the middle opening is $4a$. Minimum force needed to lift this blade-up is $\left(a=5 \mathrm{cm}\right)$

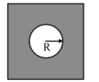
There is a uniform rectangular wire frame having a thin film of soap solution. A massless thin wire of radius $R$ and area of cross section $A$ is placed on the surface of film, and inside portion of the film is pricked. If surface tension of soap solution is $S$ and Young's modulus of wire is $Y$ then change in radius of the wire is:

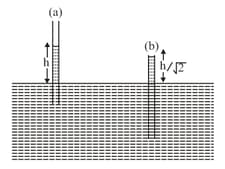
Two different vertical positions $\left(a\right)$ & $\left(b\right)$ of a capillary tube are shown in figure with the lower end inside water. For position $\left(a\right)$, contact angle is $\frac{\pi }{4}$ rad & water rises to height $h$ above the surface of water while for position $\left(b\right)$ height of the tube outside water is kept insufficient & equal to $\frac{h}{\sqrt{2}}$ ,then contact angle in radian becomes:

A water jet of radius $R$ is shown in the figure. The force between the part $1$ and part $2$ at the section $ABCD$ due to the surface tension is : (Assume that, $T$ is surface tension)

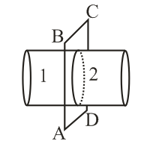
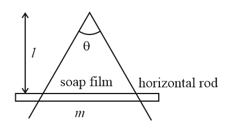
A wire is bend at an angle $\theta$. A rod of mass $m$ can slide along the bended wire without friction as shown in figure. If a soap film is maintained in the frame and frame is kept in a vertical position and rod is in equilibrium. If rod is displaced slightly in vertical direction. The time period of small oscillation is $a\pi \sqrt{\frac{bl}{g}}$ sec. where $a$ and $b$ are constant number then $a+b$ is

A metallic wire of density $d$ floats horizontally in water. The maximum radius of the wire such that it may not sink will be (surface tension of water $=T$) (Neglect buoyant force)