Embibe Experts Solutions for Chapter: Simple Harmonic Motion, Exercise 3: Exercise-3

The oscillation of a body on a smooth horizontal surface is represented by the equation, $x=A\cos \left(\omega t\right)$, where $x=$displacement at time $t$, $\omega$$=$frequency of oscillation. Which one of the following graph shows correctly the variation $a$ with $t$?

Here, $a=$ acceleration at time $t$,

$T=$ time period.

A particle moves with simple harmonic motion in a straight line. In first $\tau \mathrm{s}$ after starting from rest it travels a distance $a$ and in the next $\tau \mathrm{s}$ it travels $2a$ in the same direction, then

For a simple pendulum, a graph is plotted between its kinetic energy $\left(KE\right)$ and potential energy $\left(PE\right)$ against its displacement $d$. Which one of the following represents these correctly? (The graphs are schematic and not drawn to scale)

A particle performs simple harmonic motion with amplitude $A$. Its speed is trebled at the instant that it is at distance $\frac{2A}{3}$ from equilibrium position. The new amplitude of the motion is

A particle is executing simple harmonic motion with a time period $T$.  At time $t=0$, it is at its position of equilibrium. The kinetic energy-time graph of the particle will look like :

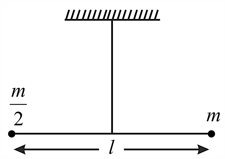
Two masses $\mathrm{m}$ and $\frac{\mathrm{m}}{2}$ are connected at the two ends of a massless rigid rod of length $\ell$. The rod is suspended by a thin wire of torsional constant $k$ at the centre of mass of the rod-mass system (see figure). Because of torsional constant$k,$the restoring torque is $\tau =k\theta$. for angular displacement $\theta .$ If the rod is rotated by $\theta$  and released, the tension in it when it passes through its mean position will be : 

A wooden cube (density of wood $d$) of side $l$ floats in a liquid of density $\rho$ with its upper and lower surfaces horizontal. If the cube is pushed slightly down and released, it performs a simple harmonic motion of period $T$. Then, $T$ is equal to: 

A cylindrical plastic bottle of negligible mass is filled with $310 \mathrm{ml}$ of water and left floating in a pond with still water. If pressed downward slightly and released, it starts performing simple harmonic motion at angular frequency, $\omega$. If the radius of the bottle is $2.5 \mathrm{cm}$ then $\omega$ is close to (density of water $={10}^3 \mathrm{kg} {\mathrm{m}}^{-3}$)