Embibe Experts Solutions for Chapter: Kinematics, Exercise 4: Exercise-4
Embibe Experts Physics Solutions for Exercise - Embibe Experts Solutions for Chapter: Kinematics, Exercise 4: Exercise-4
Attempt the free practice questions on Chapter 4: Kinematics, Exercise 4: Exercise-4 with hints and solutions to strengthen your understanding. Beta Question Bank for Engineering: Physics solutions are prepared by Experienced Embibe Experts.
Questions from Embibe Experts Solutions for Chapter: Kinematics, Exercise 4: Exercise-4 with Hints & Solutions
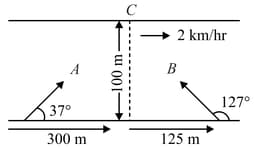
Two swimmers start a race. One who reaches the point first on the other bank wins the race. A makes his strokes in a direction of to the river flow with velocity relative to water. makes his strokes in a direction to the river flow with same relative velocity. River is flowing with speed of and is wide. Who will win the race? Compute the time taken by and to reach the point if the speed of and on the ground are and respectively.
A swimmer starts to swim from point to cross a river. He wants to reach point on the opposite side of the river. The line makes an angle with the river flow as shown. The velocity of the swimmer in still water is same as that of the water
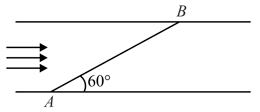
(i) In what direction should he try to direct his velocity? Calculate angle between his velocity and river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.
Hailstones falling vertically with speed of hit the windscreen of a moving car and rebound elastically. Find the velocity of the car if the driver find the hailstones rebound vertically after striking. Windscreen makes an angle with the horizontal.
A shell is fired from a point at an angle of with a speed of & it strikes a horizontal plane through , at a point . The gun is fired a second time with the same angle of elevation but a different speed . If hits the target which starts to rise vertically from with a constant speed at the same instant as the shell is fired, find .
Two inclined planes and having inclinations and respectively, intersect each other at as in figure. A particle is projected from point with velocity along a direction perpendicular to plane . If the particle strikes the plane perpendicularly at . Calculate
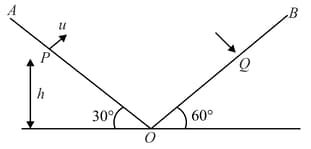
(i) Time of flight.
(ii) Velocity with which particle strikes the plane .
(iii) Vertical height of from
(iv) Maximum height from attained by the particle.
(v) Distance .
A stone is projected from the point of a ground in such a direction so as to hit a bird on the top of a telegraph post of height and then attain the maximum height above the ground. If at the instant of projection, the bird were to fly away horizontally with a uniform speed, find the ratio between the horizontal velocities of the bird and the stone, if the stone still hits the bird while descending.
A projectile is launched at an angle from a cliff of height above the sea level. If it falls into the sea at a distance from the base of the cliff, show that its maximum height above the sea level is
A particle takes seconds less and acquires a velocity , higher at one place than at another place in falling through the same distance. If the product of the acceleration due to gravity at these two places is . Find value of .
