Embibe Experts Solutions for Chapter: Simple Harmonic Motion, Exercise 1: Exercise-1

The magnitude of average acceleration in half time period in a simple harmonic motion is

A particle performs S.H.M. with time period $T$. The time taken by the particle to move from half the amplitude to the maximum displacement is

A particle of mass $m$ executing SHM makes $f$ oscillation per second. The difference of its kinetic energy when all the centre, and when at a distance $x$ from the centre is

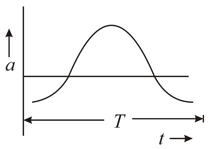
Acceleration $a$ and time period $T$ of a body in S.H.M. is given by a curve shown below. Then corresponding graph between kinetic energy $KE$ and time $t$ is correctly represented by

A particle is performing S.H.M. with acceleration $a=8{\pi }^2-4{\pi }^{2}x$ where $x$ is coordinate of the particle w.r.t. the origin. The parameters are in S.I. units. The particle is at rest at $x=-2$ at $t=0$.

An oscillation is described by the equation $x=A\sin 2\pi {\gamma }_{1}t$ where $A$ changes with time according to the law $A=A_0\left(1+\cos 2\pi {\gamma }_{2}t\right)$ where $A_0$ is constant. Find the ratio of frequencies of harmonic oscillations forming oscillation 

Vertical displacement of a plank with a body of mass '$m$' on it is varying according to law $y=\sin \omega t+\sqrt{3} \cos \omega t$. The minimum value of $\omega$ for which the mass just breaks off the plank and the moment it occurs first after $t=0$ are given by: ($y$ is positive vertically upwards)

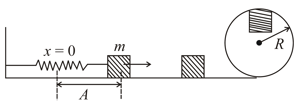
A block of mass $m$ is placed on a level frictionless table. The block is attached to a horizontally aligned spring fixed with its other end is vibrating in a horizontal plane with the period $T$. Suddenly at the instant of time when the spring comes to the position of equilibrium and becomes unstretched the block disconnects from the spring and continues sliding across the frictionless surface away from the until it encounters a loop of radius $R$. What must be the amplitude of vibrations of the blocks on the spring in order for the block to complete one loop without falling down?