Embibe Experts Solutions for Chapter: Simple Harmonic Motion, Exercise 3: Exercise-3

The particle executing $\mathrm{SHM}$ in a straight line has velocities $8 \mathrm{m} {\mathrm{s}}^{-1}$, $7 \mathrm{m} {\mathrm{s}}^{-1}$. $4 \mathrm{m} {\mathrm{s}}^{-1}$at three points distance one metre fro each other. If maximum velocity of the particle is $\sqrt{13\alpha }$. Find $\alpha$

The displacement of a particle varies with time as $x=\left(12 \sin \omega t-16 {\sin }^3\omega t\right) \mathrm{cm}$. If its motion is $\mathrm{SHM}$, if maximum acceleration $9a{\omega }^2$. Find a

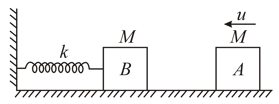
In the figure shown, the block $A$ collides with the block $B$ and after collision they stick together. Calculate the amplitude of resultant vibration in $\mathrm{cm}$. Given $m=1 \mathrm{kg}, k=2 \mathrm{N} {\mathrm{cm}}^{-1}, u=6 \mathrm{cm} {\sec }^{-1}$

A block of mass $1 \mathrm{kg}$ hangs without vibrating at the end of a spring with a force constant $1 \mathrm{N} {\mathrm{m}}^{-1}$ attached to the ceiling of an elevator. The elevator is rising with an upward acceleration of $\frac{g}{4}$. The acceleration of the elevator suddenly ceases. If amplitude of the resulting oscillations is $2A$. Find $A$.

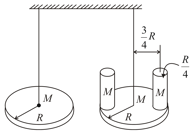
The two torsion pendula differ only by the addition of cylindrical masses as shown in the figure. The radius of each additional mass is $1/4$ the radius of the disc. Each cylinder and disc have equal mass. The ratio of time periods of the two torsion pendula is $p$. Then $27{\mathrm{p}}^2$ is.

Two particles $A$ and $B$ execute SHM along the same line with the same amplitude $\mathrm{a}$and same frequency about same equilibrium position $O$. If the phase difference between them is $\varphi =2 {\sin }^{-1}\left(0.9\right)$, if maximum distance between the two is $2\alpha a$. Find $\alpha$

A body executing $\mathrm{S}.\mathrm{H}.\mathrm{M}.$ has its velocity $10 \mathrm{cm} {\mathrm{s}}^{-1}$ and $7 \mathrm{cm} {\mathrm{s}}^{-1}$ when its displacement from the mean position are $3 \mathrm{cm}$ and $4 \mathrm{cm}$ respectively. Calculate the length of the path.

A particle is oscillating in a straight line about a centre of force $O$, towards which when at a distance $x$ the force is $m{n}^{2}x$ where $m$is the mass, $n$ a constant. The amplitude is $a=15 \mathrm{cm}$. When at a distance $\frac{a\sqrt{3}}{2}$ from $O$ the particle receives a blow in the direction of motion which generates a velocity na. If the velocity is away from $O$, if new amplitude is $15\sqrt{\alpha }$. Find $\alpha$.