Embibe Experts Solutions for Chapter: Gravitation, Exercise 4: BEGINNER'S BOX - 4

If earth describes an orbit round the sun of double its present radius, what will be the year on earth ?

If the gravitational force were to vary inversely as $m^{\mathrm{th}}$ power of the distance, then the time period of a planet in a circular orbit of radius $r$ around the sun will be proportional to:

A planet is revolving around the sun in an elliptical orbit. Its closest distance from the sun is $r_{\min }$. The farthest distance from the sun is $r_{\max }$. If the orbital angular velocity of the planet when it is nearest to the sun is $\omega$, then the orbital angular velocity at the point when it is at the farthest distance from the sun is:-

The time period of revolution of moon around the earth is 28 days and radius of its orbit is 4 × 10⁵ km.
If G = 6.67 × 10^–11 Nm²/kg² then find the mass of the earth.

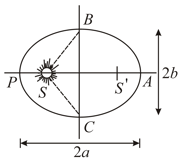
Let the speed of the planet at the perihelion P in Fig. be v_P and the Sun-planet distance SP be r_p. Relate (r_p, v_P) to the corresponding quantities at the aphelion (r_A, v_A). Will the planet take equal times to traverse BAC and CPB ?

Asatellite moves in a circular orbit around the earth. The radius of this orbit is one half that of the moon’s orbit. Find the time in which the satellite completes one revolution.

A small satellite revolves round a planet in an orbit just above planet’s surface. Taking the mean density of planet as $\rho$, calculate the time period of the satellite.

An object weighs $10 \mathrm{N}$ at the North Pole of the earth. In a geostationary satellite distant $7R$ from the centre of the earth (of radius $R$), the true weight and the apparent weight are, respectively,