Embibe Experts Solutions for Chapter: Work, Energy and Power, Exercise 2: Exercise 2

The potential energy of a $1 \mathrm{kg}$ particle free to move along the $x$-axis is given by $V\left(x\right)=\left(\frac{x^4}{4}-\frac{x^2}{2}\right) \mathrm{J}$. The total mechanical energy of the particle is $2 \mathrm{J}$. Then, the maximum speed (in $\mathrm{m} {\mathrm{s}}^{-1}$) is

Ten litre of water per second is lifted from a well through $10 \mathrm{m}$ and delivered with a velocity of $10 \mathrm{m} {\mathrm{s}}^{-1}$. If $g=10 \mathrm{m} {\mathrm{s}}^{-2}$, then the power of the motor is

A block of mass $0.50 \mathrm{kg}$ is moving with a speed of $2.00 \mathrm{m} {\mathrm{s}}^{-1}$ on a smooth surface. It strikes another mass of $1.00 \mathrm{kg}$ and then they move together as a single body. The energy loss during the collision is

An athlete in the Olympic game covers a distance of $100 \mathrm{m}$ in $10 \mathrm{s}$. His kinetic energy can be estimated to be in the range

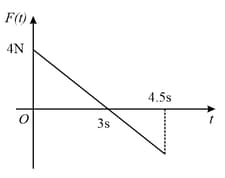
A block of mass $2 \mathrm{kg}$ is free to move along the $x$-axis. It is at rest and from $t=0$ onwards, it is subjected to a time-dependent force $F\left(t\right)$ in the $x$ direction. The force $F\left(t\right)$ varies with $t$ as shown in the figure. The kinetic energy of the block after $4.5 \mathrm{second}$ is

The potential energy function for the force between two atoms in a diatomic molecule is approximately given by, $U\left(x\right)=\frac{a}{x^{12}}-\frac{b}{x^6}$, where $a$ and $b$ are constants and $x$ is the distance between the atoms. If the dissociation energy of the molecule is $D=\left[U_{\left(x=\infty \right)}-U_{\mathrm{at} \mathrm{equilibrium}}\right]$, $D$ is

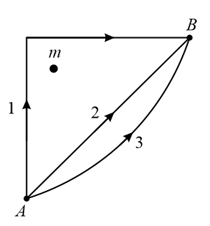
If $W_1, W_2$ and $W_3$ represent the work done in moving a particle from $A$ to $B$ along three different paths $1, 2$ and $3$, respectively (as shown), in the gravitational field of a point mass $m$, find the correct relation between $W_1, W_2$ and $W_3$.

At time $t=0 \mathrm{s}$, particle starts moving along the $x$-axis. If its kinetic energy increases uniformly with time $t$, the net force acting on it must be proportional to