Embibe Experts Solutions for Chapter: Counting, Exercise 1: EXERCISE

How many ways can a student schedule $3$ mathematics courses - algebra, geometry, and number theory in a $6$-period day if no two mathematics courses can be taken in consecutive periods? (What courses the student takes during the other $3$ periods is of no concern here).

There are $20$ students participating in an after-school program offering classes in yoga, bridge, and painting. Each student must take at least one of these three classes, but may take two or all three. There are $10$ students taking yoga, $13$ taking bridge, and $9$ taking painting. There are $9$ students taking at least two classes. How many students are taking all three classes?

Five friends sat in a movie theater in a row containing $5$ seats, numbered $1$ to $5$ from left to right. (The directions "left" and "right" are from the point of view of the people as they sit in the seats.) During the movie Asha went to the lobby to get some popcorn. When she returned, she found that Bhawna had moved two seats to the right, Chetna had moved one seat to the left, and Divya and Esha had switched seats, leaving an end seat for Asha. In which seat had Asha been sitting before she got up?

A palindrome number is the same either read from left to right or right to left, for example. $121$ is a palindrome number. Total possible $5$-digit palindrome numbers can be written as $10a.$ Find the value of $a$

Five students $A, B, C, D$ and $E$ form a team to take part in a $5$-leg relay competition. If $A$ cannot run the first leg and $D$ cannot run the last leg, how many ways can we arrange them to run the relay?

Different positive $3$-digit integers are formed from the five digits $1, 2, 3, 5, 7,$ and repetitions of the digits are allowed. As an example, such positive $3$-digit integers include $352, 577, 111,$ etc. Now, the sum of all the distinct positive $3$-digit integers formed in this way is written as $ABC50$. Find $A+B+C$.

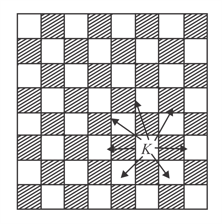
As shown in the picture, the knight can move to any of the indicated squares of the $8\times 8$ chessboard in $1$ move. If the knight starts from the position shown, find the number of possible landing positions after $20$ consecutive moves.

There are $N$ number of $11$-digit positive integers such that the digits from left to right are non-decreasing. (For example, $\left(12345678999, 55555555555, 23345557889\right).$ Find the sum of all the digits of $N$.