Embibe Experts Solutions for Chapter: Electric Charges and Fields, Exercise 1: Exercise

Two small spheres 18cm apart have equal negative charges and repel each other with the force $6\times {10}^{-8}N$. Find the total charge on two spheres.

Two charged particles having charge $2·0\times {10}^{-8} \mathrm{C}$ each are joined by an insulating string of length $1 \mathrm{m}$ and the system is kept on a smooth horizontal table. Find the tension in the string.

Two small sphere, each having a mass of $20 \mathrm{g}$, are suspended from a common point by two insulating strings of length $40 \mathrm{cm}$ each. The spheres are identically charged and the separation between the balls at equilibrium is found to be $4 \mathrm{cm}$. Find the charge on each sphere.

A particle having a charge of $2.0\times {10}^{-4} \mathrm{C}$ is placed directly below and at a separation of $10 \mathrm{cm}$ from the bob of a simple pendulum at rest. The mass of the bob is $100 \mathrm{g}$. What charge should the bob be given so that the string becomes loose?

An electric charge $Q$ is divided into two part $Q_{1 }$and $Q_2$ which then are kept at a distance $r$ apart. What will be the condition for the force between them to be maximum.

Three charges $+2q, -q$ are $\mathit{-}q$  are placed at the vertices $A, B$ and $C$ respectively of an equilateral triangle $ABC$ of side $a$. Find the magnitude of dipole moment of this system.

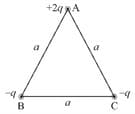
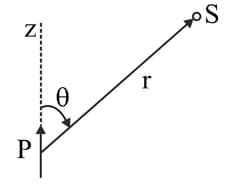
Demonstrate that the potential of the field generated by a dipole, with electric moment $\overrightarrow{\mathit{P}}$, may be represented as $\mathrm{\phi }=\frac{\overrightarrow{p}·\overrightarrow{r}}{4\mathrm{\pi }{\epsilon }_0{r}^3}$, where $\overrightarrow{\mathit{r}}$ is the radius vector. Using this expression, find the magnitude of the electric field strength vector as a function of $r$ and $\mathrm{\theta }$.

Each of the two long parallel threads carry a uniform charge $\lambda$ per unit length. The threads are separated by a distance $l$. Find the maximum magnitude of the electric field strength in the symmetry plane of this system, located between the threads.