Embibe Experts Solutions for Chapter: Thermodynamics, Exercise 1: Exercise 1

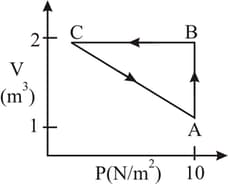
An ideal gas is taken through the cycle $A\to B\to C\to A$ as shown in the fig. If the net heat supplied to the gas in the cycle is $5 \mathrm{J},$ the work done by the gas in the process $C\to A$ is:

Consider $R$ to be the universal gas constant. Given that, the amount of heat needed to raise the temperature of $2\mathrm{ }\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{s}$ of an ideal monatomic gas from $273\mathrm{ }\mathrm{K}$ to $373\mathrm{ }\mathrm{K}$ when no work is done is $n\times R$. Then $n$ is

$32 \mathrm{g}$ of ${\mathrm{O}}_2$ is contained in a cubical container of side $1 \mathrm{m}$ and maintained at a temperature of $127 °\mathrm{C}$. The isothermal bulk modulus of elasticity of the gas in terms of universal gas constant $R$ is $aR$. Find the value of $a$.

An ideal gas $\left(\frac{C_p}{C_v}=\gamma \right)$ is taken through a process in which the pressure and the volume vary such that $P=\alpha V^{\beta }$. The value of $\beta$, for which molar heat capacity of gas is zero, is $n\gamma$. Value of $n$, is

An ideal monoatomic gas undergoes a process such that its internal energy relates to the volume as $U=a\sqrt{V}$, where $a$ is a constant. Molar specific heat of the gas is $nR.$ Value of $n,$ is

Two moles of a diatomic ideal gas is taken through a process, $P=\frac{\alpha }{T}$, where $\alpha$ is a positive constant. Temperature of gas is increased from $T_0$ to $2T_0$, work done by the gas is $NR{T}_0$. Value of $N$, is

A cyclic process $ABC$ is performed on one mole of an ideal gas, $T_A=350 \mathrm{K}$ and $T_B=450 \mathrm{K}$. A total of $1200 \mathrm{J}$ of heat is withdrawn from the gas in the complete cycle. Work done by the gas during process $B\to C$ is $-45n \mathrm{J}$. Value of $n$ is $\left[R=8.25{\mathrm{JK}}^{-1}{ \mathrm{mol}}^{-1}\right]$

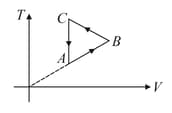
$N$ moles of a diatomic gas performs a work $\frac{Q}{3}$ on its surrounding when $Q$ amount of heat is supplied to the gas. Molar heat capacity of the process is $n R$. Value of $n$, is