Exercise
Embibe Experts Mathematics Solutions for Exercise
Simple step-by-step solutions to Exercise questions of Triangles from THINK ABOVE AND BEYOND MATHEMATICS PRACTICE BOOKS. Also get 3D topic explainers, cheat sheets, and unlimited doubts solving on EMBIBE.
Questions from Exercise with Hints & Solutions
There is a street merchant who sells toys for kids. Every day he used to display the toys on a blanket whose length is feet and feet. As his business was in profit, he decided to display more toys for sale. For this purpose, he bought a new similar blanket with length feet. Find the ratio of perimeter to the area of bigger blanket he had.
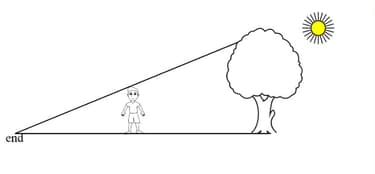
Ravi is tall. He wants to find the height of a tree in his backyard. From the tree's base he walked along the tree's shadow to a position where the end of his shadow exactly overlaps the end of the tree’s shadow. He is now from the end of the shadow. How tall is the tree? Express your answer in metre(m).
Two poles of heights and are erected upright on the ground and ropes are stretched from the top of each to the foot of the other.
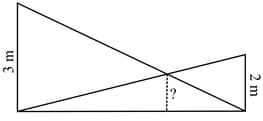
The height above the ground at which the ropes cross each other is?
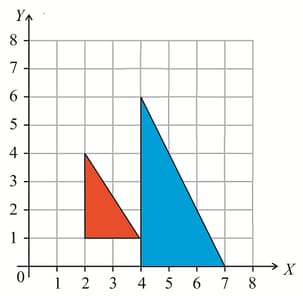
Anish is asked to enlarge the red triangle with scale factor about a centre of enlargement at . He draws the blue triangle. Explain why Anish is not correct.
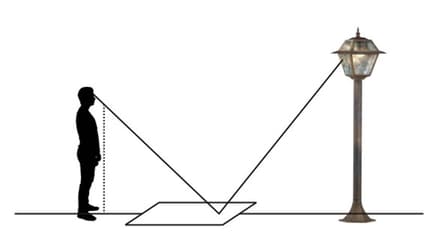
Just as in mathematics, principles in physics often lead to other useful results. Fermat's principle states that light travels in a path that requires the least time. How light behaves when reflected off a surface (called the law of reflection) can be derived from this principle. The law of reflection states that when light hits a reflective surface at an angle, it will reflect off that surface at the same angle.
Describe how this information could be used to find the height of the lamppost.
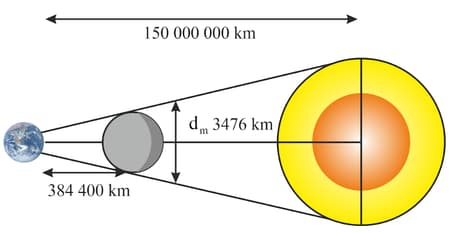
During a solar eclipse, the moon passes between the sun and earth and covers sun almost entirely despite being considerably smaller. Why the moon covers almost all part of the sun during an eclipse. Take diameter of the sun as
Megha made two similar kites. The diagonal of the bigger kite is times the diagonal of the smaller kite.
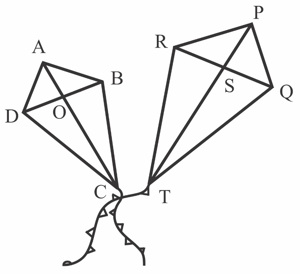
In the smaller kite, the two diagonals are: and . Find the length of the bigger diagonal of the bigger kite (in ).
