G L Mittal and TARUN MITTAL Solutions for Chapter: Simple Harmonic Motion, Exercise 3: FOR DIFFERENT COMPETITIVE EXAMINATIONS

a particle of mass m moves on the $X$-axis in a potential of the form $U\left(x\right)=k{x}^2$, it performs simple harmonic motion. The corresponding time period is proportional to $\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}$ as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of $\mathrm{x}=0$  in a way different from ${\mathrm{kx}}^2$ and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the $X$-axis. Its potential energy is $\mathrm{U}\left(\mathrm{x}\right)=\alpha x^4 (\mathrm{a}>0) \mathrm{for} \left|\mathrm{x}\right|$ near the origin and becomes a constant equal to ${\mathrm{U}}_0 \mathrm{for} \left|\mathrm{x}\right|>{\mathrm{x}}_0$(see figure below)

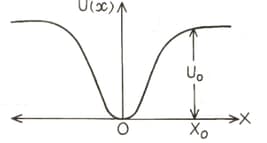
If the total energy of the particle is $\mathrm{E}$, it will perform periodic motion only if

A particle of mass m moves on the $X$-axis in a potential of the form $U\left(x\right)=k{x}^2$ , it performs simple harmonic motion. The corresponding time period is proportional to$\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}$, as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of $\mathrm{x}=0$  in a way different from ${\mathrm{kx}}^2$and its total energy is such that the particle does not escape to infinity. Consider a particle of mass $\mathrm{m}$ moving on the $X$-axis. Its potential energy is $\mathrm{U}\left(\mathrm{x}\right)=\alpha x^4(\alpha >0) \text{for} \left|\mathrm{x}\right|$ near the origin and becomes a constant equal to ${\mathrm{U}}_0\mathrm{for}\left|\mathrm{x}\right|>{\mathrm{x}}_0$(see figure below)

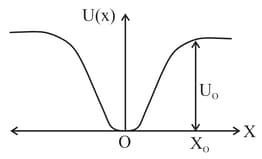
For periodic motion of small amplitude $\mathrm{A}$, the time period $\mathrm{T}$ of the particle is proportional to:

A particle of mass m moves on the X-axis in a potential of the form U (x) = k x, it performs simple harmonic motion. The corresponding time period is proportional to$\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}$ as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of $\mathrm{x}=0$  in a way different from ${\mathrm{kx}}^2$ and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the X-axis. Its potential energy is $\mathrm{U}\left(\mathrm{x}\right)={\mathrm{ax}}^4(\mathrm{a}>0) \mathrm{for} \left|\mathrm{x}\right|$ near the origin and becomes a constant equal to ${\mathrm{U}}_0 \mathrm{for} \left|\mathrm{x}>\right|>{\mathrm{x}}_0$ (see figure below)

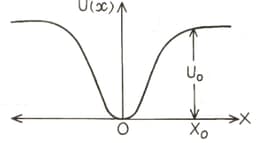
Acceleration of this particle for $\left|\mathrm{x}\right|>{\mathrm{x}}_0$  is 

A particle of mass $m$ is attached to one end of a massless spring of force constant$\mathrm{k}$, lying on a frictionless horizontal plane. The other end of the spring is fixed. The particle starts moving horizontally from its equilibrium position at time $\mathrm{t}=0$ with an initial velocity ${\mathrm{u}}_0$ when the speed of the particle is $0.5{\mathrm{u}}_0$ .It collides elastically with a rigid wall. After this collision.

The time-period of a pendulum suspended from the ceiling of a stationary train is $\mathrm{T}$. When the train starts moving with an acceleration $\mathrm{a}$, then, the time-period of pendulum:

A second pendulum is placed in a space laboratory orbiting around the earth at a height $3{\mathrm{R}}_{\mathrm{e}}$ from the earth’s surface, where $R_e$ is earth’s radius. The period of the pendulum will be$:$

A piece of wire is bent in the space of a parabola $\mathrm{y}={\mathrm{kx}}^2(\mathrm{T} \mathrm{axis} \mathrm{vertical})$ with a bead of mass $\mathrm{m}$ on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the $\mathrm{x}$-axis with a constant acceleration  $\mathrm{a}$. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the  $\mathrm{y}$-axis is:

An ideal gas enclosed in a vertical cylindrical container supports a freely moving piston of mass $\mathrm{M}$. The piston and the cylinder have equal cross-sectional area $\mathrm{A}$ When the piston is in equilibrium, the volume of the gas is ${\mathrm{V}}_0$ and its pressure is ${\mathrm{P}}_0$ The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency.