H C Verma Solutions for Chapter: Centre of Mass, Linear Momentum, Collision, Exercise 4: EXERCISES

A cart of mass $M$ is at rest on a frictionless horizontal surface and a pendulum bob of mass $m$ hangs from the roof of the cart. The string breaks, the bob falls on the floor, makes several collisions on the floor and finally lands up in a small slot made in the floor. The horizontal distance between the string and the slot is $L.$ Find the displacement of the cart during this process.

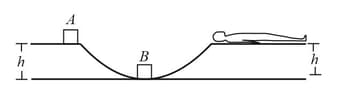
The track shown in the figure is frictionless. The block $B$ of mass $2m$ is lying at rest and the block $A$ of mass $m$ is pushed along the track with some speed. The collision between $A$ and $B$ is perfectly elastic. With what velocity should the block $A$ be started to get the sleeping man awakened?

A uniform chain of mass $M$ and length $L$ is held vertically in such a way that its lower end just touches the horizontal floor. The chain is released from rest in this position. Any portion that strikes the floor comes to rest. Assuming that the chain does not form a heap on the floor, calculate the force exerted by it on the floor when a length $x$ has reached the floor.

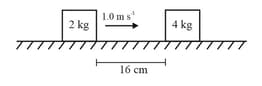
The friction coefficient between the horizontal surface and each of the blocks shown in the figure is $0.20$. The collision between the blocks is perfectly elastic. Find the separation between the two blocks when they come to rest. Take $g=10 \mathrm{m} {\mathrm{s}}^{-2}$.

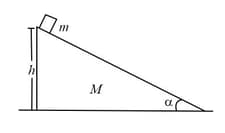
A block of mass $m$ is placed on a triangular block of mass $M,$ which in turn is placed on a horizontal surface, as shown in the figure. Assuming frictionless surfaces, find the velocity of the triangular block when the smaller block reaches the bottom end.

A small block of super dense material has a mass of $3\times {10}^{24} \mathrm{kg}.$ It is situated at a height $h$ (much smaller than the Earth's radius) from where it falls on the Earth's surface. Find its speed when its height from the Earth's surface has reduced to $\frac{h}{2}$. The mass of the Earth is $6\times {10}^{24} \mathrm{kg}$.

A body of mass $m$ makes an elastic collision with another identical body at rest. Show that if the collision is not head-on, the bodies go at right angles to each other after the collision.

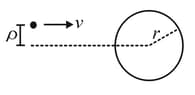
A small particle travelling with a velocity $v$ collides elastically with a spherical body of equal mass and of radius $r$, initially kept at rest. The centre of this spherical body is located at a distance $\rho (<r)$, away from the direction of motion of the particle (see the figure below). Find the final velocity of the particle and the spherical body.