H C Verma Solutions for Chapter: Work and Energy, Exercise 4: EXERCISES

A block of mass of $2.0 \mathrm{kg}$ kept at rest on an inclined plane of inclination $37°$is pulled up the plane by applying a constant force of $20 \mathrm{N}$ parallel to the incline. The force acts for one second. Find the work done by the force of gravity in that one second if the work done by the applied force is $40 \mathrm{J}$.

A block of mass $2 \mathrm{kg}$ kept at rest on an inclined plane of inclination $37°$ is pulled up the plane by applying a constant force of $20 \mathrm{N}$ parallel to the incline. The force acts for one second. Find the kinetic energy of the block at the instant the force ceases to act. Take $\mathrm{g}=10 \mathrm{m} {\mathrm{s}}^{-2}$.

A heavy particle is suspended by a $1.5 \mathrm{m}$ long string. It is given a horizontal velocity of $\sqrt{57} \mathrm{m} {\mathrm{s}}^{-1}$.

(a) Find the angle made by the string with the upward vertical, when it becomes slack.
(b) Find the speed of the particle at this instant.
(c) Find the maximum height reached by the particle over the point of suspension. Take $\mathrm{g}=10 \mathrm{m} {\mathrm{s}}^{-2}$

A simple pendulum of length $L$ having a bob of mass $m$ is deflected from its rest position by an angle $\text{θ}$ and released. The string hits a peg which is fixed at a distance $x$ below the point of suspension and the bob starts going in a circle centered at the peg.

(a) Assuming that initially the bob has a height less than the peg, show that the maximum height reached by the bob equals its initial height.

(b) If the pendulum is released with $\text{θ}=90°$ and $x=L/2$ find the maximum height reached by the bob above its lowest position before the string becomes slack.
(c) Find the minimum value of $x/L$ for which the bob goes in a complete circle about the peg when the pendulum is released from $\text{θ}=90°$

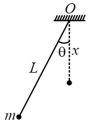
A particle of mass $m$ is kept on a fixed, smooth sphere of radius $R$ at a position, where the radius through the particle makes an angle of $30°$ with the vertical. The particle is released from this position.
(a) What is the force exerted by the sphere on the particle just after the release?
(b) Find the distance travelled by the particle before it leaves contact with the sphere.

A particle of mass $m$ is kept on the top of a smooth sphere of radius $R$. It is given a sharp impulse which imparts it a horizontal speed $v$.

(a) Find the normal force between the sphere and the particle just after the impulse.

(b) What should be the minimum value of $v$ for which the particle does not slip on the sphere?
(c) Assuming the velocity $v$ to be half the minimum calculated in part (b), find the angle made by the radius through the particle with the vertical when it leaves the sphere.

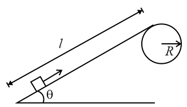
Figure shows a smooth track which consists of a straight inclined part of length $l$ joining smoothly with the circular part. A particle of mass $m$ is projected up the incline from its bottom.
(a) Find the minimum projection-speed $v_0$ for which the particle reaches the top of the track.

(b) Assuming that the projection-speed is $2v_0$ and that the block does not lose contact with the track before reaching its top, find the force acting on it when it reaches the top.

(c) Assuming that the projection-speed is only slightly greater than $v_0$, where will the block lose contact with the track?

A chain of length $l$ and mass $m$ lies on the surface of a smooth sphere of radius $R>l$ with one end tied to the top of the sphere.
(a) Find the gravitational potential energy of the chain with reference level at the centre of the sphere.
(b) Suppose the chain is released and slides down the sphere. Find the kinetic energy of the chain, when it has slid through an angle $\theta$
(c) Find the tangential acceleration $\frac{dv}{dt}$ of the chain when the chain starts sliding down.