H K Dass, Rama Verma and, Bhagwat Swarup Sharma Solutions for Chapter: Similar Triangles, Exercise 8: REVISION EXERCISE

The diagonals of a trapezium $ABCD$, in which $AB\parallel DC$, intersects at $O$. If $AB=2CD$, then find the ratio of areas of triangles $AOB$ and $COD$.

In a triangle $ABC$, the midpoints of sides $AB, BC$ and $CA$ are $D, E$ and $F$ respectively. Find the ratio of areas of $△DEF$ and $△ABC$.

In the given figure, $XY\parallel AC$ and $XY$ divides triangular region $ABC$ into two parts equal in area. If the ratio of $\frac{AX}{AB}=\frac{\sqrt{2}-1}{\sqrt{k}}$, then find the value of $k$.

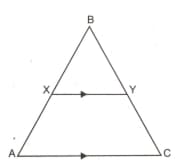
In the figure, if $AD\perp BC$. Prove that $A{B}^2+C{D}^2=B{D}^2+A{C}^2$.

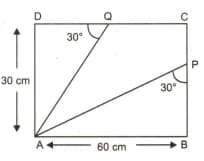
In the given figure, $ABCD$ is a rectangle in which segments $AP$ and $AQ$ are drawn. Find the length $\left(AP+AQ\right)$

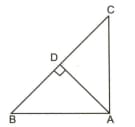
Prove that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of other two sides.

Prove that the ratio of the areas of two similar triangles is equal to the squares of the ratio of their corresponding sides.

State and prove converse of Pythagoras theorem.