I E Irodov Solutions for Chapter: OPTICS, Exercise 1: PHOTOMETRY AND GEOMETRICAL OPTICS
I E Irodov Physics Solutions for Exercise - I E Irodov Solutions for Chapter: OPTICS, Exercise 1: PHOTOMETRY AND GEOMETRICAL OPTICS
Attempt the practice questions on Chapter 5: OPTICS, Exercise 1: PHOTOMETRY AND GEOMETRICAL OPTICS with hints and solutions to strengthen your understanding. Problems in General Physics solutions are prepared by Experienced Embibe Experts.
Questions from I E Irodov Solutions for Chapter: OPTICS, Exercise 1: PHOTOMETRY AND GEOMETRICAL OPTICS with Hints & Solutions
Find the optical power and the focal lengths
of a thin glass lens, in a liquid with refractive index and refractive index of glass in air is , if its optical power in air is ;
of a thin symmetrical biconvex glass lens, with air on one side and water on the other side, if the optical power of that lens in air is .
By means of plotting, find
the path of a ray of light beyond thin converging and diverging lenses (where is the optical axis, and are the front and rear focal points);
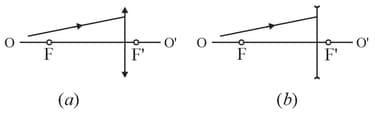
the position of a thin lens and its focal points, if the position of the optical axis and the positions of the conjugate points (see figure) are known; the media on both sides of the lenses are identical;
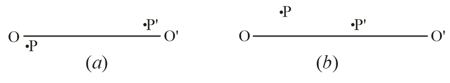
the path of ray beyond the converging and diverging lenses (Figure), if the path of ray and the positions of the lens and of its optical axis are all known; the media on both sides of the lenses are identical.
A thin converging lens with focal length projects the image of an object on a screen removed from the lens by a distance . Then the screen was drawn closer to the lens by a distance . By what distance should the object be shifted for its image to become sharp again?
A source of light is located at a distance from a screen. A thin converging lens provides the sharp image of the source when placed between the source of light and the screen at two positions. Determine the focal length of the lens if
the distance between the two positions of the lens is ,
the transverse dimensions of the image at one position of the lens are greater than those at the other position.
A thin converging lens is placed between an object and a screen whose positions are fixed. There are two positions of the lens at which the sharp image of the object is formed on the screen. Find the transverse dimension of the object if at one position of the lens the image dimension equals and at the other, .
There are two thin symmetrical lenses, one is converging with refractive index , and the other is diverging with refractive index . Both the lenses have the same curvature radius of their surfaces, equal to . The lenses were put close together and submerged into water. What is the focal length of this system in water? Refractive index of water in air is .
Determine the focal length of a concave spherical mirror which is manufactured in the form of a thin symmetric biconvex glass lens one of whose surfaces is silvered. The curvature radius of the lens surface is .
Figure illustrates an aligned system consisting of three thin lenses. The system is located in air. Determine,
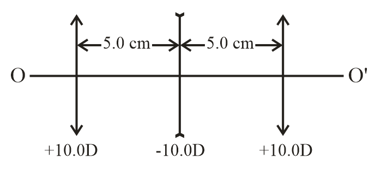
the position of the point of convergence of a parallel ray incoming from the left after passing through the system,
the distance between the first lens and a point lying on the axis to the left of the system, at which that point and its image are located symmetrically with respect to the lens system.
