G L Mittal and TARUN MITTAL Solutions for Chapter: Rotational Motion of a Rigid Body : Moment of Inertia, Exercise 3: FOR DIFFERENT COMPETITIVE EXAMINATIONS

The dancer on ice spins faster when she folds her arms. This is due to

A thin circular ring of mass M and radius $\mathrm{r}$ is rotating about its axis with a constant angular velocity $\omega$. Two objects, each of mass $\mathrm{m}$, are attached gently to the opposite ends of the diameter of the ring. The wheel now rotates with an angular velocity

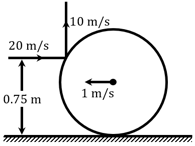
A thin ring of mass $2\mathrm{kg} , \mathrm{radius} 0.5 \mathrm{m}$ is rolling without slipping on a horizontal plane with velocity $1\mathrm{m}/\mathrm{s}$. A small ball of mass $0.1\mathrm{kg}$ , moving with velocity $20 \mathrm{m}/\mathrm{s}$ in the opposite direction, hits the ring at a height of $0.75 \mathrm{m}$ and goes vertically up with velocity $10 \mathrm{m}/\mathrm{s}$  immediately after the collision, choose the correct statement :

A mass $m$ hangs with help of a string wrapped around a pulley on a frictionless bearing. The pulley has mass $\mathrm{m}$ and radius $\mathrm{R}$ . Assuming pulley to be a perfect uniform circular disc, the acceleration of the mass, $\mathrm{m}$ if the string does not slip on the pulley, is:

A solid cylinder of mass $50 \mathrm{kg}$and radius $0.5\mathrm{m}$s free to rotate about the horizontal axis. A massless string is wound round the cylinder with one end attached to it and other end hanging freely. Tension in the string required to produce an angular acceleration of $2 \mathrm{rev}/{\mathrm{s}}^2$ is:

The ratio of the accelerations for a solid sphere $(\mathrm{mass} \mathrm{m} \mathrm{radius} \mathrm{R})$ rolling down an incline of angle $\mathrm{\theta }$ without slipping, and slipping down the incline without rolling is

A round uniform body of radius $\mathrm{R}$, mass $M$ and moment of inertia $I$ rolls down (without slipping) an inclined plane making an angle theta with the horizontal. Then its acceleration

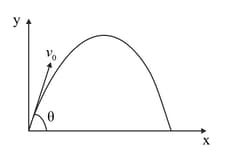
A small particle of mass m is projected at an angle $\theta$ with the x-axis with an initial velocity ${\mathrm{v}}_0$ in the x-y plane as shown in the figure. At a time$\mathrm{t}<\frac{{\mathrm{v}}_0\mathrm{sin\theta }}{\mathrm{g}}$​, the angular momentum of the particle is