Jan Dangerfield, Stuart Haring and, Julian Gilbey Solutions for Exercise 3: EXERCISE 5B

A mass of $2 \mathrm{kg}$ is held on a rough horizontal table. The coefficient of friction between the table and the mass is $0.05.$ The $2 \mathrm{kg}$ mass is attached by a light inextensible string to a mass of $3 \mathrm{kg}$ and by a second light inextensible string to a mass of $4 \mathrm{kg}.$ The strings pass over smooth pulleys at the edges of the table. The $3 \mathrm{kg}$ mass hangs on one side of the table and the $4 \mathrm{kg}$ mass hangs on the other side of the table. The system is released from rest. Find the tension in each string. (The acceleration of the moving mass is $1 \mathrm{m} {\mathrm{s}}^{-2}$.)

A wedge has two smooth sloping faces; one face makes an angle $30°$ with the horizontal and the other makes an angle $60°$ with the horizontal. A small smooth pulley is fixed at the apex of the wedge. A light inextensible string passes over the pulley and lies parallel to the faces of the wedge. At each end of the string there is a particle of mass $0.3 \mathrm{kg}.$ The system is released from rest.

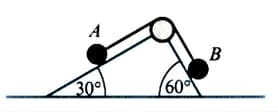
Work out the resultant horizontal force on each of the particles.

A box of mass $3 \mathrm{kg}$ hangs from a light inextensible string, which passes over a smooth pulley fixed below a beam and then under a smooth cylinder of mass $4 \mathrm{kg}$ that is free to move. The other end of the string is fixed to the beam. The system is released from rest.

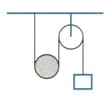
Explain why the magnitude of the acceleration of the cylinder is half the magnitude of the acceleration of the box.

A box of mass $3 \mathrm{kg}$ hangs from a light inextensible string, which passes over a smooth pulley fixed below a beam and then under a smooth cylinder of mass $4 \mathrm{kg}$ that is free to move. The other end of the string is fixed to the beam. The system is released from rest.

Find the acceleration of the box, including its direction.

A horizontal shelf of mass $1 \mathrm{kg}$ hangs from four strings. A book of mass $0.2 \mathrm{kg}$ sits on the shelf. Four strings are attached to the underside of the shelf and a second horizontal shelf of mass $1 \mathrm{kg}$ hangs from these strings.

What modelling assumptions can be made about the strings?

A horizontal shelf of mass $1 \mathrm{kg}$ hangs from four strings. A book of mass $0.2 \mathrm{kg}$ sits on the shelf. Four strings are attached to the underside of the shelf and a second horizontal shelf of mass $1 \mathrm{kg}$ hangs from these strings.

Find the tension in each of the upper set of strings.

A horizontal shelf of mass $1 \mathrm{kg}$ hangs from four strings. A book of mass $0.2 \mathrm{kg}$ sits on the shelf. Four strings are attached to the underside of the shelf and a second horizontal shelf of mass $1 \mathrm{kg}$ hangs from these strings.

Find the tension in each of the lower set of strings.

A horizontal shelf of mass $1 \mathrm{kg}$ hangs from four strings. A book of mass $0.2 \mathrm{kg}$ sits on the shelf. Four strings are attached to the underside of the shelf and a second horizontal shelf of mass $1 \mathrm{kg}$ hangs from these strings.

The book is moved to the lower shelf. How does this change the tensions in the strings?