Jan Dangerfield, Stuart Haring and, Julian Gilbey Solutions for Exercise 1: CROSS-TOPIC REVIEW EXERCISE 2

A particle, $P$, moves on a straight track. It has displacement $s \mathrm{m}$ from a point, $O$, at time $t \mathrm{s}$, given by $s=0.12t+10-0.01t^3$ for $t>0$. Particle $Q$ moves on a track parallel to particle $P$. The acceleration, $a \mathrm{m}{ \mathrm{s}}^{-2}$, of $Q$ is given by $a=0.4-0.06t$. Both particles come to rest alongside each other. Find the displacement of $Q$ from $O$ after $10 \mathrm{s}$.

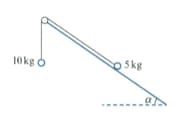
Two particles of masses $5 \mathrm{kg}$ and $10 \mathrm{kg}$ are connected by a light inextensible string that passes over a fixed smooth pulley. The $5 \mathrm{kg}$ particle is on a rough fixed slope which is at an angle of $\alpha$ to the horizontal, where $\tan \alpha =\frac{3}{4}$. The $10 \mathrm{kg}$ particle hangs below the pulley (see diagram). The coefficient of friction between the slope and the $5 \mathrm{kg}$ particle is $\frac{1}{2}$. The particles are released from rest. Find the acceleration of the particles and the tension in the string.

A particle of mass $0.1 \mathrm{kg}$ is released from rest on a rough plane inclined at $20°$ to the horizontal. It is given that, $5$ seconds after release, the particle has a speed of $2 \mathrm{m}{ \mathrm{s}}^{-1}$.

Find the acceleration of the particle and hence show that the magnitude of the frictional force acting on the particle is $0.302 \mathrm{N}$, correct to $3$ significant figures.

A particle of mass $0.1 \mathrm{kg}$ is released from rest on a rough plane inclined at $20°$ to the horizontal. It is given that, $5$ seconds after release, the particle has a speed of $2 \mathrm{m}{ \mathrm{s}}^{-1}$.

Find the coefficient of friction between the particle and the plane.

A particle $P$ moves in a straight line. It starts at a point $O$ on the line and at time $t \mathrm{s}$ after leaving $O$ it has a velocity $v \mathrm{m}{ \mathrm{s}}^{-1}$, where$v=6t^2-30t+24$.

Find the set of values of $t$ for which the acceleration of the particle is negative.

A particle $P$ moves in a straight line. It starts at a point $O$ on the line and at time $t \mathrm{s}$ after leaving $O$ it has a velocity $v \mathrm{m}{ \mathrm{s}}^{-1}$, where$v=6t^2-30t+24$.

Find the distance between the two positions at which $P$ is at instantaneous rest.

A particle $P$ moves in a straight line. It starts at a point $O$ on the line and at time $t \mathrm{s}$ after leaving $O$ it has a velocity $v \mathrm{m}{ \mathrm{s}}^{-1}$, where$v=6t^2-30t+24$.

Find the two positive values of $t$ at which $P$ passes through $O$.

Particles $P$ and $Q$ are attached to opposite ends of a light inextensible string which passes over a fixed smooth pulley. The system is released from rest with the string taut, with its straight parts vertical, and with both particles at a height of $2 \mathrm{m}$ above horizontal ground. $P$ moves vertically downwards and does not rebound when it hits the ground. At the instant that $P$ hits the ground, $Q$ is at the point $X$, from where it continues to move vertically upwards without reaching the pulley. Given that $P$ has mass $0.9 \mathrm{kg}$ and that the tension in the string is $7.2 \mathrm{N}$ while $P$ is moving, find the total distance travelled by $Q$ from the instant it first reaches $X$ until it returns to $X$.