Jan Dangerfield, Stuart Haring and, Julian Gilbey Solutions for Exercise 7: END-OF-CHAPTER REVIEW EXERCISE 4

A particle of mass $m$ is on rough, horizontal ground with coefficient of friction ${\mu }_1.$ It is initially moving at speed $u \mathrm{m}{\mathrm{s}}^{-1}.$ After a distance $x \mathrm{m}$ the surface changes to another surface with coefficient of friction ${\mu }_2.$ The particle comes to rest, having travelled a distance of $y \mathrm{m}$ on this surface. Show that  ${\mu }_2=\frac{u^2-2{\mathrm{\mu }}_1\mathrm{gx}}{2\mathrm{gy}}.$

A mass of $m$ is at rest on a plank of wood on level ground with coefficient of friction ${\mu }_1.$ One end of the plank is lifted until the mass starts to slip. The angle at which this happens is $\alpha .$

Show that ${\mu }_1=\tan \alpha .$

A mass of $m$ is at rest on a plank of wood on level ground with coefficient of friction ${\mu }_1.$ One end of the plank is lifted until the mass starts to slip. The angle at which this happens is $\alpha .$

Show that ${\mu }_1=\tan \alpha .$

The angle of the plank is then raised to an angle $\beta$ and the mass is held in place. The mass is then released and travels a distance $x$ down the slope. At the end of the slope the particle slides along the level ground, slowing down under friction where the coefficient of friction is ${\mu }_2,$ until coming to rest at a distance $y$ from the bottom of the slope. You may assume the mass starts sliding along the floor at the same speed as it has when it reaches the end of the slope.

 Show that ${\mathrm{\mu }}_2=\frac{\mathrm{x}\left(\sin \mathrm{\beta } - \tan \mathrm{\alpha }.\cos \mathrm{\beta }\right)}{\mathrm{y}}$

A particle moves up a line of greatest slope of a rough plane inclined at an angle $\alpha$ to the horizontal, where $\sin \alpha =0.28.$ The coefficient of friction between the particle and the plane is $\frac{1}{3}.$

Show that the acceleration of the particle is $-6 \mathrm{m}{\mathrm{s}}^{-2}.$

A particle moves up a line of greatest slope of a rough plane inclined at an angle $\alpha$ to the horizontal, where $\sin \alpha =0.28.$ The coefficient of friction between the particle and the plane is $\frac{1}{3}.$

Given that the particle's initial speed is $5.4 \mathrm{m}{\mathrm{s}}^{-1},$ find the distance that the particle travels up the plane.

A block of weight$7.5 \mathrm{N}$ is at rest on a plane which is inclined to the horizontal at angle $\alpha ,$ where $\tan \alpha =\frac{7}{24}.$ The coefficient of friction between the block and the plane is $\mu .$ A force of magnitude $7.2 \mathrm{N}$ acting parallel to a line of greatest slope is applied to the block. When the force acts up the plane (see Fig. $1$) the block remains at rest.

Show that $\mu ⩾\frac{17}{24}$.

When the force acts down the plane (see Fig. $2$) the block slides downwards.

A block of weight$7.5 \mathrm{N}$ is at rest on a plane which is inclined to the horizontal at angle $\alpha ,$ where $\tan \alpha =\frac{7}{24}.$ The coefficient of friction between the block and the plane is $\mu .$ A force of magnitude $7.2 \mathrm{N}$ acting parallel to a line of greatest slope is applied to the block. When the force acts up the plane (see Fig. $1$) the block remains at rest.

Show that $\mu <\frac{31}{24}.$

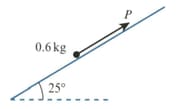
The diagram shows a particle of mass $0.6 \mathrm{kg}$ on a plane inclined at $25°$ to the horizontal. The particle is acted on by a force of magnitude $P \mathrm{N}$ directed up the plane parallel to a line of greatest slope. The coefficient of friction between the particle and the plane is $0.36.$ Given that the particle is in equilibrium, find the set of possible values of $P$