Jan Dangerfield, Stuart Haring and, Julian Gilbey Solutions for Exercise 7: EXERCISE 1D

The sketch shows a displacement-time graph of a car slowing down with constant acceleration before coming to rest at a set of traffic lights.

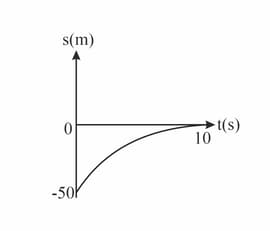
By comparison with the equation $s=s_0+ut+\frac{1}{2}a{t}^2,$ Find the initial speed and acceleration of the car.

A cyclist is stationary when a second cyclist passes, travelling at a constant speed of $8 \mathrm{m}{ \mathrm{s}}^{-1}.$ The first cyclist then accelerates for $5 \mathrm{s}$ At a constant rate of $2 \mathrm{m}{ \mathrm{s}}^{-2}$ Before continuing at constant speed until overtaking the second cyclist. By sketching both graphs, find the equations of the two straight-line sections of the graphs and, hence, find how long it is before the first cyclist overtakes the second.

A leader in a race has $500 m$ to go and is running at a constant speed of $4 m s^{-1}$, but with $100 m$ to go increases her speed by a constant acceleration of $0.1 m s^{-1}$. The second runner is $100 m$ behind the leader when the leader has $500 m$ to go, and running at $3.8 m s^{-1}$ when she starts to accelerate at a constant rate. Find the minimum acceleration she needs in order to win the race.

A van driver wants to pull out from rest onto a road where cars are moving at a constant speed of $20 \mathrm{m}{ \mathrm{s}}^{-1}.$ When there is a large enough gap between cars, the van driver pulls out immediately after one car passes. She then accelerates at a constant rate of $4 \mathrm{m}{ \mathrm{s}}^{-2}$ until moving at $20 \mathrm{m}{ \mathrm{s}}^{-1}.$ To do this safely the car behind must always be at least $10 \mathrm{m}$ away. Find the minimum length of the gap between the cars for the van driver to pull out.

A police motorcyclist is stationary when a car passes, driving dangerously at a constant speed of $40 \mathrm{m}{ \mathrm{s}}^{-1}.$ At the instant the car passes, the motorcyclist gives chase, accelerating at $2.5 \mathrm{m}{ \mathrm{s}}^{-2}$ until reaching a speed of $50 \mathrm{m}{ \mathrm{s}}^{-1}$ before continuing at a constant speed. Show that the motorcyclist has not caught the car by the time he reaches top speed. Find how long after the car initially passed him the motorcyclist catches up to the car.

The front of a big wave is approaching a beach at a constant speed of $11.6{ \mathrm{ms}}^{-1}.$ When it is $30 \mathrm{m}$ away from a boy on the beach, the wave starts decelerating at a constant rate of $1.6 \mathrm{m}{ \mathrm{s}}^{-2}$ and the boy walks away from the sea at a constant speed of $2 \mathrm{m}{ \mathrm{s}}^{-1}.$ Show that the wave will not reach the boy and find the minimum distance between the boy and the wave.

Swimmers going down a waterslide $30 \mathrm{m}$ long push themselves off with an initial speed of between $1 \mathrm{m}{ \mathrm{s}}^{-1}$ and $2 \mathrm{m}{ \mathrm{s}}^{-1}.$ They accelerate down with constant acceleration $0.8 \mathrm{m}{ \mathrm{s}}^{-2}$ for the first $20 \mathrm{m}$ before more water is added and the acceleration is $1 \mathrm{m}{ \mathrm{s}}^{-2}$ for the last $10 \mathrm{m}$ of the slide. For safety there must be at least $5 \mathrm{s}$ between swimmers arriving at the bottom of the slide. Find the minimum whole number of seconds between swimmers being allowed to start the slide.

A ball is projected in the air with initial speed $u$and goes up and down with acceleration $g$downwards. A timer is at a height $h$. It records the time from the ball being projected until it passes the timer on the way up as $t_1$ and on the way down as $t_2$. Show that the total of the two times is independent of $h$ and that the initial speed can be calculated as $u = \frac{g\left(t_1+t_2\right)}{2}$. Show also that the difference between the times is given by $\frac{2\sqrt{u^2-2gh}}{g}$. Hence, find a formula for $h$in terms of $t_{1,} t_2$ and $g$.