K A Tsokos Solutions for Chapter: Mechanics, Exercise 1: Test yourself

The graph shows the variation of the velocity of a moving object with time. Draw the graph showing the variation of the position of the object with time ( assuming a zero initial position).

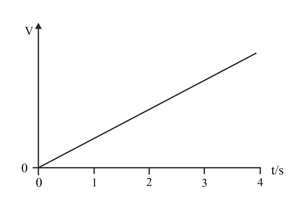
The graph shows the variation of the velocity of a moving object with time. Draw the graph showing the variation of the acceleration of the object with time.

Your brand new convertible Ferrari is parked $15 \mathrm{m}$ from its garage when it begins to rain. You do not have time to get the keys,so you begin to push the car towards the garage. The maximum acceleration you can give the car is $2.0 \mathrm{m} {\mathrm{s}}^{-2}$ by pushing and $3.0 \mathrm{m} {\mathrm{s}}^{-2}$ by pulling back on the car. Find the least time it takes to put the car in the garage. (Assume that the car, as well as the garage, are point objects.)

A cruel hunter takes aim horizontally at a chimp that is hanging from the branch of a tree, as shown in the diagram. The chimp lets go of the branch as soon as the hunter pulls the trigger. Treating the chimp and the bullet as point particles, determine if the bullet will hit the chimp.

A stone is thrown at a speed of $20.0 \mathrm{m} {\mathrm{s}}^{-1}$ at an angle of ${48}^{\circ }$ to the horizontal from the edge of a cliff $60.0 \mathrm{m}$ above the surface of the sea. Calculate the velocity with which the stone hits the sea.

A stone is thrown at a speed of $20.0 \mathrm{m} {\mathrm{s}}^{-1}$ at an angle of ${48}^{\circ }$ to the horizontal from the edge of a cliff $60.0 \mathrm{m}$ above the surface of the sea. Discuss qualitatively the effect of air resistance on the final velocity of the stone.

State what is meant by terminal speed.

A ball is dropped from rest. The force of air resistance in the ball is proportional to the ball's speed. Explain why the ball will reach terminal speed.