Name: Division of a Trinomial by a Trinomial
Uploaded: 2019-07-19
Duration: 3 min 36 s
Description: Can we divide a polynomial by another polynomial to get the quotient polynomial and the remainder polynomial? Let's explore this concept in this video.

Question

Write the relation below in algebra and see if it gives a polynomial. Give reasons for your conclusion also.

Two poles of heights $3 m$ and $4 m$ are erected upright on the ground, $5 m$ apart. A rope is to be stretched from the top of one pole to some point on the ground and from there to the top of the other pole:

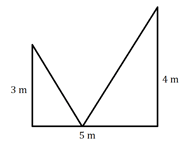
The relation between the distance of the point on the ground from the foot of a pole and the total length of the rope.

Accepted Answer

Here, we have

Let the distance of the point $B$ on ground be $x m$ from the $3 m$ pole.

So, the distance of the point on ground from $4 m$ pole is $(5 - x) m$ .

Now the length of the rope is $A B + B C$ .

By Pythagoras theorem,

$A B^{2} = A D^{2} + D B^{2}$

$\Rightarrow A B^{2} = 3^{2} + x^{2}$

$\Rightarrow A B = \sqrt{9 + x^{2}}$

Similarly,

$B C^{2} = 4^{2} + {(5 - x)}^{2}$

$\Rightarrow B C^{2} = 16 + 25 - 10 x + x^{2}$

$\Rightarrow B C = \sqrt{x^{2} - 10 x + 41}$

So, the length of the rope $= \sqrt{9 + x^{2}} + \sqrt{x^{2} - 10 x + 41}$

We can express this as ${(9 + x^{2})}^{\frac{1}{2}} + {(x^{2} - 10 x + 41)}^{\frac{1}{2}}$

Now, we know all the exponents in the algebraic expression must be non-negative integers in order for the algebraic expression to be a polynomial.

Thus, the expression is not a polynomial.

Kerala Board Solutions for Chapter: Polynomials, Exercise 2: Exercise 2

Kerala Board Mathematics Solutions for Exercise - Kerala Board Solutions for Chapter: Polynomials, Exercise 2: Exercise 2

Questions from Kerala Board Solutions for Chapter: Polynomials, Exercise 2: Exercise 2 with Hints & Solutions

Learn and Prepare for any exam you want !