Kesab Chandra Nag Solutions for Exercise 1: EXERCISE-2

Prove that if two medians of triangle be equal, then it is an isosceles triangle.

 In the trapezium $ABCD$, $AB\parallel DC$. The diagonals $AC$ and $BD$ of it intersects each other at $O$. Prove that $∆AOD=∆BOC$.

$D, E$ and $F$ are the midpoints of the sides $AB$. $AC$ and $BC$ of the $∆ABC$. Prove that $DF$ and $AE$ bisects each other.

 $E$ is the midpoint of the median $AD$ of the $∆ABC$. Extended $BE$ intersects $AC$ at $F$. Prove that $AF=\frac{1}{3}AC$.

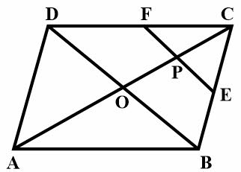
$\mathrm{D}$ and $\mathrm{E}$ are the midpoints of $\mathrm{AB}$ and $\mathrm{AC}$ respectively of the $∆\mathrm{ABC}$. $\mathrm{AP}$ is the median of $\mathrm{BC}$. $\mathrm{AP}$ intersects $\mathrm{DE}$ at $\mathrm{Q}$. Prove that $\mathrm{DQ}=\mathrm{QE}$ and $\mathrm{AQ}=\mathrm{QP}$.

 Prove that the line segments obtained by joining the midpoints of the opposite sides of any quadrilateral bisects each other.

Prove that the quadrilateral formed by joining the midpoints successively of any quadrilateral is also a parallelogram.  Also, prove that the perimeter of that quadrilateral is equal to the sum of its diagonals.

$E$ and $F$ are the midpoints of the sides $BC$ and $CD$ of the parallelogram $ABCD$. $EF$ intersects the diagonal $AC$ at $P$. Prove that $AC=4PC$.