Kumar Mittal Solutions for Exercise 1: QUESTIONS

A plane surface of area $10{\mathrm{m}}^2$ is placed in the X-Z plane where an electric field $\overrightarrow{\mathrm{E}}=(2\hat{\mathrm{i}}+4\hat{\mathrm{j}}+7\hat{\mathrm{k}}){\mathrm{NC}}^{-1}$ exists. Calculate the electric flux passing through the surface.

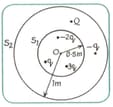
In the figure charges are enclosed by spherical surfaces $S_1$ and $S_2$  If the electric flux through surface $S_2$ is four times that of electric flux through$S_1$, find relation between $Q$ and $q$.

State Gauss’ theorem in electrostatics.
Apply this theorem to derive an expression for the electric intensity due to an infinite sheet of charge and hence deduce the expression for electric intensity due to two parallel oppositely charged thin infinite sheets of charge at a point

(ii) Outside the sheets.

Using Gauss’ theorem, derive an expression for the electric field intensity due to a charged thin spherical shell at Surface point.

Draw the graph showing the variation of electric field intensity obtained as above with distance from the centre.

Using Gauss’ theorem derive an expression for the electric intensity due to a charged thin spherical shell at

internal point.

Draw the graph showing the variation of electric intensity obtained as above with distance from the centre.

A point-charge produces an electric flux of $-750{\mathrm{Nm}}^2{\mathrm{C}}^{-1}$ through a spherical Gaussian surface of $10 \mathrm{cm}$ radius with centre at the charge.

What is the magnitude of point-charge?

A sphere of metal has a radius of $12 \mathrm{cm}$ and carries a charge of $1.6\times {10}^{-7}\mathrm{C}$, distributed uniformly on its surface. Calculate the electric field intensity at a point just outside the sphere. 

A sphere of metal has a radius of $12 \mathrm{cm}$ and carries a charge of $1.6\times {10}^{-7}\mathrm{C}$, distributed uniformly on its surface. Calculate the electric field intensity at a point $18 \mathrm{cm}$ from the centre of the sphere.