L.A.Sena Solutions for Chapter: Molecular Physics and Thermodynamics, Exercise 1: Exercise
L.A.Sena Physics Solutions for Exercise - L.A.Sena Solutions for Chapter: Molecular Physics and Thermodynamics, Exercise 1: Exercise
Attempt the practice questions on Chapter 2: Molecular Physics and Thermodynamics, Exercise 1: Exercise with hints and solutions to strengthen your understanding. A Collection of Questions and problems in Physics solutions are prepared by Experienced Embibe Experts.
Questions from L.A.Sena Solutions for Chapter: Molecular Physics and Thermodynamics, Exercise 1: Exercise with Hints & Solutions
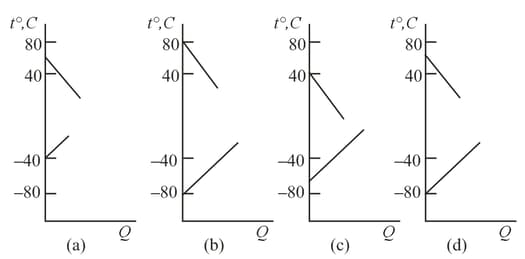
When ice with a temperature below is mixed with water with a temperature above , there are four possibilities: the ice melts and the final temperature is above , the water freezes and the final temperature is below , part of the ice melts and the temperature of the mixture becomes , and part of the water freezes and the temperature of the mixture becomes . On the horizontal axis we lay off the amount of heat that the water gives off in cooling and freezing (the upper straight lines) and the amount of heat that the ice absorbs in heating and melting (the lower straight lines). The scale along the horizontal axis is arbitrary, that is, the scale value is not specified. The temperature (in degrees Celsius) is laid off on the vertical axis. Find the final result of mixing whose beginning is shown in each figure. When either all the water freezes or all the ice melts, determine the final temperature.
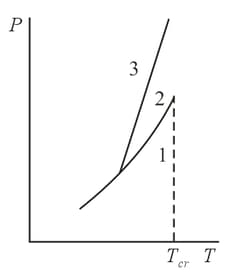
A phase diagram represents the relationship between the temperature and pressure at the boundary that separates two phases. To which phases do the regions and correspond?
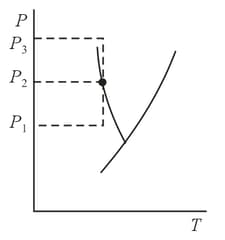
The phase diagram of water is shown schematically in the figure. Using this diagram, explain this particular dependence of the melting point of ice on the external pressure.
The compressibility of a liquid does not remain constant under pressure variations. How, knowing the dependence of compressibility on pressure within a certain pressure interval from to , can we find the ratio of volumes at these values of pressure?
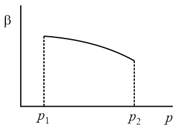
As is known, the density of water at first grows when water is heated from but then, at , begins to drop, as shown in the figure. Does the explanation of this lie in the fact that in introducing the metric system of units the weight of a definite volume of water at was taken as the unit of weight (subsequently this was taken as a unit of mass)?
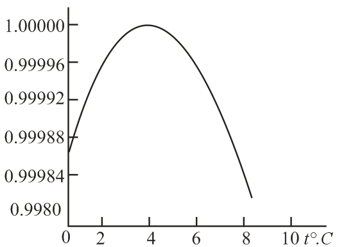
The wall of a house consists of two layers with different thermal conductivity coefficients. The temperature of the outer wall is and that of the inner wall is . Temperature variations inside the wall are shown in the figure. What layer, the inner or the outer, has a higher thermal conductivity coefficient?
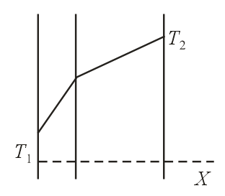
A rod with a cross-sectional area and initial length is elongated by due to a tensile stress. The modulus of longitudinal elasticity of the material of the rod, or Young's modulus, is . Find the bulk energy density for the deformation of the rod.
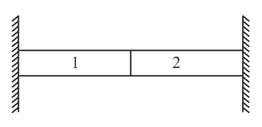
Two bars and of the same cross-sectional area and the same length but made of different materials are clamped between two undeformable walls. The materials of the bars differ in mechanical and thermal properties. What must be the relationship between Young's moduli and the linear coefficients of thermal expansion so that heating the bars does not change the position of the boundary between them? Under what conditions does the deformability of the walls have no effect on the result?