M L Aggarwal Solutions for Exercise 1: EXERCISE 14
M L Aggarwal Mathematics Solutions for Exercise - M L Aggarwal Solutions for Exercise 1: EXERCISE 14
Attempt the practice questions from Exercise 1: EXERCISE 14 with hints and solutions to strengthen your understanding. Understanding ICSE Mathematics Class 9 solutions are prepared by Experienced Embibe Experts.
Questions from M L Aggarwal Solutions for Exercise 1: EXERCISE 14 with Hints & Solutions
Any point is taken on the side of a triangle and is produced to such that . Prove that area of triangle area of triangle .
is a rectangle and is the mid-point of is produced to meet at . Prove that area of rectangle area of the triangle .
In the figure given below, the perimeter of the parallelogram is . Calculate the lengths of the sides of the parallelogram.
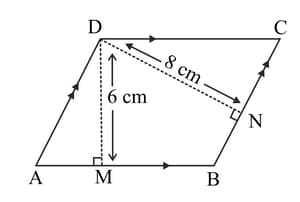
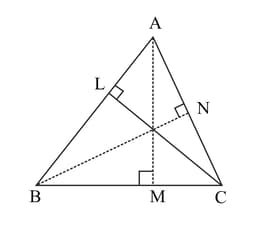
in the given figure perimeter of a triangle is . if the lengths of the altitude and are , respectively, calculate the length of the sides of triangle .
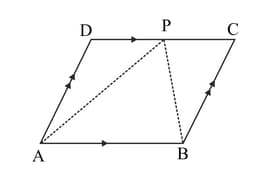
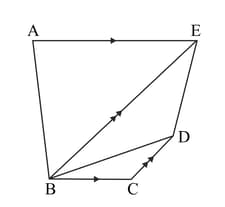
In the figure given below is parallelogram. is the point on the side , such that the area of the triangle and the area of the triangle. Find the .
In the figure given below, and . Prove that area of area of .
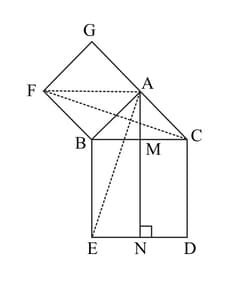
In the figure given below, is right angled triangle at . is a square on the side and is a square on the hypotenuse . If , prove that .
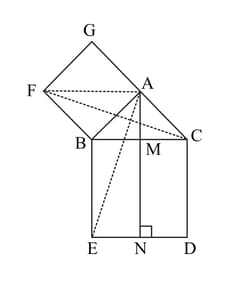
In the figure given below, is right angled triangle at . is a square on the side and is a square on the hypotenuse . If , prove that area of square area of rectangle .