Maharashtra Board Solutions for Chapter: Magnetic Fields due to Electric Current, Exercise 3: Exercises

 A moving coil galvanometer has been fitted with a rectangular coil having 50 turns and dimensions $5 \mathrm{cm} \times 3 \mathrm{cm}$. The radial magnetic field in which the coil is suspended is of $0.05\mathrm{Wb}/{\mathrm{m}}^2$. The torsional constant of the spring is $1.5\times {10}^{-9}\mathrm{Nm}/$degree. Obtain the current required to be passed through the galvanometer so as to produce a deflection of $30°$. 

A solenoid of length $\mathrm{\pi m}$ and $5 \mathrm{cm}$ in diameter has winding of 1000 turns and carries a current of $5 \mathrm{A}$. Calculate the magnetic field at its centre along the axis.

A toroid of narrow radius of $10 \mathrm{cm}$ has 1000 turns of wire. For a magnetic field of $5\times {10}^{-2}\mathrm{T}$ along its axis, how much current is required to be passed through the wire? 

In a cyclotron protons are to be accelerated. Radius of its D is $60 \mathrm{cm}$. and its oscillator frequency is $10 \mathrm{MHz}$. What will be the kinetic energy of the proton thus accelerated? 

Proton mass $=1.67\times {10}^{-27}\mathrm{kg}$ $\left.\mathrm{e}=1.60\times {10}^{-19}\mathrm{C},1\mathrm{eV}=1.6\times {10}^{-19}\mathrm{J}\right)$

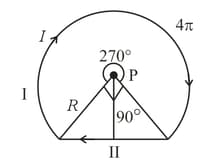
A wire loop of the form shown in the figure carries a current I. Obtain the magnitude and direction of the magnetic field at P. Given: $\mathrm{B}=\frac{{\mathrm{\mu }}_0\mathrm{I}}{4\mathrm{\pi R}}\sqrt{2}$

Two long parallel wire's going into the plane of the paper are separated by a distance R, and carry a current I each in the same direction. Show that the magnitude of the magnetic field at a point P equidistant from the wires and subtending angle $\mathrm{\theta }$ from the plane containing the wires, is $\mathrm{B}=\frac{{\mathrm{\mu }}_0}{\mathrm{\pi }}\frac{\mathrm{I}}{\mathrm{R}}\sin 2\mathrm{\theta }$. What is the direction of the magnetic field?

Figure shows a section of a very long cylindrical wire of diameter a, carrying a current I. The current density which is in the direction of the central axis of the wire varies linearly with radial distance r from the axis according to the relation $\mathrm{J}={\mathrm{J}}_0\mathrm{r}/\mathrm{a}.$Obtain the magnetic field B inside the wire at a distance r from its centre.

In the figure below, what will be the magnetic field B inside the wire at a distance r from its axis, if the current density J is uniform across the cross section of the wire?