Manipur Board Solutions for Chapter: Triangles, Exercise 1: EXERCISE 7.1

Line segment $AB$ is parallel to another equal line segment $CD$. $O$ is the midpoint of $AD$. Prove that $O$ is also the midpoint of $BC$.

In $∆ABC$, the bisector $AD \text{of} \angle A$ is perpendicular to side $BC$. Prove that $∆ABC$ is isosceles.

$P$ is a point equidistant from two lines $l \text{and} m$ intersecting at a point $A$. Prove that the line $AP$ bisects the angle between the lines. 

$ABCD$ is a rectangle. $P, Q, R \text{and} S$ are the mid-points of $AB, BC, CD \text{and} DA$ respectively. Prove that $PQRS$ is a rhombus. 

Prove that the diagonals of a rhombus bisect each other at right angles. 

$ABCD$ is a parallelogram and $AC$ is one of its diagonals. Prove that $∆ABC\cong ∆ADC$.

$AB \text{and} AC$ are equal sides of an isosceles $∆ABC$. If the bisectors of $\angle ABC$ and $\angle ACB$ intersect each other at $O$, prove $∆AOB\cong ∆AOC$. 

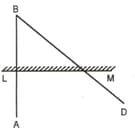
The image of an object placed at a point $A$ before a plane mirror $LM$ is seen at the point $B$ by an observer at $D$ as in the adjoining figure. Prove that the image is as far behind the mirror as the object is in front of the mirror.