Telangana Board Solutions for Chapter: Triangles, Exercise 2: EXERCISE

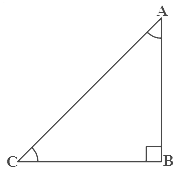
In right triangle $\mathrm{ABC}$, right angle is at $C$, $M$ is the mid-point of hypotenuse $AB$. $C$ is joined to $M$ and produced to a point $D$ such that $\mathrm{DM}=\mathrm{CM}$. Point $D$ is joined to point $B$ (see figure). Show that: $\angle \mathrm{DBC}$ is a right angle.

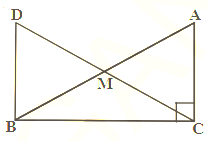
In right triangle $\mathrm{ABC}$, right angle is at $C$, $M$ is the mid-point of hypotenuse $AB$. $C$ is joined to $M$ and produced to a point $D$ such that $\mathrm{DM}=\mathrm{CM}$. Point $D$ is joined to point $B$ (see figure). Show that: $∆\mathrm{DBC}\cong ∆\mathrm{ACB}$.

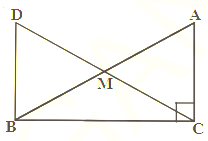
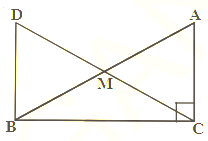
In the right triangle $\mathrm{ABC}$, right angle is at $C$, $M$ is the midpoint of hypotenuse $AB$. $C$ is joined to $M$ and produced to a point $D$ such that $\mathrm{DM}=\mathrm{CM}$. Point $D$ is joined to point $B$ (see figure). Show that: $\mathrm{CM}=\frac{1}{2}\mathrm{AB}$.

In the adjacent figure $\mathrm{ABCD}$ is a square and $∆\mathrm{APB}$ is an equilateral triangle. Prove that $∆\mathrm{APD}\cong ∆\mathrm{BPC}$.

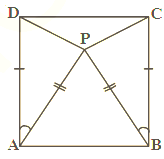
In the given figure, $∆\mathrm{ABC}$ is isosceles as $\overline{\mathrm{AB}}=\overline{\mathrm{AC}}, \overline{\mathrm{BA}}$ and $\overline{CA}$ are produced to $Q$ and $P$ such that $\overline{AQ}=\overline{AP}$. Show that $\overline{PB}=\overline{QC}$.

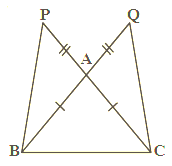
In the given $∆\mathrm{ABC}$, $D$ is the midpoint of $BC$. $\mathrm{DE}\perp \mathrm{AB}, \mathrm{DF}\perp \mathrm{AC}$ and $DE=DF$. Show that $∆\mathrm{BED}\cong ∆\mathrm{CFD}$.

If the bisector of an angle of a triangle also bisects the opposite side, prove that the triangle is isosceles.

In the given figure, $\mathrm{ABC}$ is a right triangle and right angled at $\mathrm{B}$ such that $\angle \mathrm{BCA}=2\angle \mathrm{BAC}$. Show that hypotenuse $\mathrm{AC}=2\mathrm{BC}$.